题目内容
9.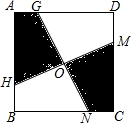 如图,点O是边长为2的正方形ABCD的对称中心,过点O作OM⊥ON,分别交正方形边于M、N、G、H,则当OM、ON绕点O旋转时,图中的阴影部分是否关于O点为中心对称?这两部分的面积是否改变?请说明理由.
如图,点O是边长为2的正方形ABCD的对称中心,过点O作OM⊥ON,分别交正方形边于M、N、G、H,则当OM、ON绕点O旋转时,图中的阴影部分是否关于O点为中心对称?这两部分的面积是否改变?请说明理由.
分析 连接AC,根据点O是边长为2的正方形ABCD的对称中心,得到AC过点O,推出△AOG≌△CON,得到OG=OC,同理△AOH≌△COM,得到OH=OM,于是得到图中的阴影部分是否关于O点为中心对称,两部分的面积不改变.
解答 解: 连接AC,∵点O是边长为2的正方形ABCD的对称中心,
连接AC,∵点O是边长为2的正方形ABCD的对称中心,
∴AC过点O,
∴AO=CO,∠GAO=∠NCO=45°,
在△AOG与△CON中,$\left\{\begin{array}{l}{∠GAO=NCO}\\{AO=CO}\\{∠AOG=∠CON}\end{array}\right.$,
∴△AOG≌△CON,
∴OG=ON,
同理△AOH≌△COM,
∴OH=OM,
∴图中的阴影部分是否关于O点为中心对称,两部分的面积不改变.
点评 本题考查了中心对称,全等三角形的判定与性质,能证得三角形全等是解题的关键.

练习册系列答案
相关题目
8.为了测试某种型号汽车的性能(车速不超过140km/h),对汽车的“刹车距离”进行测试,测试数据如下表:
(1)观察表格中的数据,估计刹车距离关于刹车时的车速的函数的类型,并确定一个满足这些数据的函数的表达式;
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
| 刹车时的车速x(km/h) | 0 | 10 | 20 | 40 | 60 |
| 刹车距离y(m) | 0 | 0.3 | 1.0 | 3.6 | 7.8 |
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
4.下列角度中不是多边形内角和的只有( )
| A. | 540° | B. | 720° | C. | 960° | D. | 1080° |
1.若0<α<30°,则sinα,cosα,tanα的大小关系是( )
| A. | sinα<cosα<tanα | B. | sinα<tanα<cosα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
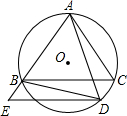 ⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.
⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.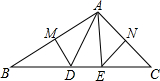 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,已知△ADE的周长为12cm,∠BAC=110°,求BC的长及∠DAE的度数.
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,已知△ADE的周长为12cm,∠BAC=110°,求BC的长及∠DAE的度数.