题目内容
若
-
=-2，则x2-
的值为 ．
| x |
| 1 | ||
|
| 1 |
| x2 |
考点：完全平方公式
专题：计算题
分析：两边平方得出(
-
)2=(-2)2=4，展开后求出x+
=6，求出(
+
)2=8，求出
+
=2
，代入x2-
=(x+
)(
+
)(
-
)=-24
求出即可．
| x |
| 1 | ||
|
| 1 |
| x |
| x |
| 1 | ||
|
| x |
| 1 | ||
|
| 2 |
| 1 |
| x2 |
| 1 |
| x |
| x |
| 1 | ||
|
| x |
| 1 | ||
|
| 2 |
解答：解：平方得：(
-
)2=(-2)2=4，
展开后x+
-2=4，
∴x+
=6，
∴x+
+2=8，
即(
+
)2=8，
∴
+
=2
，
∴x2-
=(x+
)(
+
)(
-
)=-24
，
故答案为：-24
．
| x |
| 1 | ||
|
展开后x+
| 1 |
| x |
∴x+
| 1 |
| x |
∴x+
| 1 |
| x |
即(
| x |
| 1 | ||
|
∴
| x |
| 1 | ||
|
| 2 |
∴x2-
| 1 |
| x2 |
| 1 |
| x |
| x |
| 1 | ||
|
| x |
| 1 | ||
|
| 2 |
故答案为：-24
| 2 |
点评：本题考查了完全平方公式和平方差公式的应用，能分别求出x+
、
+
、
-
的值是解此题的关键，本题题型较好，但是有一定的难度．
| 1 |
| x |
| x |
| 1 | ||
|
| x |
| 1 | ||
|
练习册系列答案
科学实验活动册系列答案
相关题目
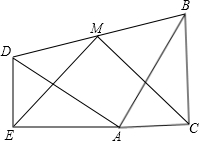如图，两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起，∠DEA=∠ACB=90°，∠DAE=∠ABC=30°，E、A、C三点在一条直线上，连接BD，取BD中点M，连接ME、MC，试判断△EMC的形状，并说明理由．下列图形中，是轴对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
平面直角坐标系中，半径为5的⊙M与x轴交于A、B两点，且AB=8，与y轴切于点C，若双曲线在反比例函数y=-
的图形上的一个点是（ ）
| 5 |
| x |
| A、（2，2.5） |
| B、（-2.5，2.5） |
| C、（-2.5，2） |
| D、（2.5，2.5） |
