题目内容
如图,AB∥CD,直线PQ截AB、CD于点E、F,点M是直线PQ上的一个动点(点M不与E、F重合),点N在射线FC上.
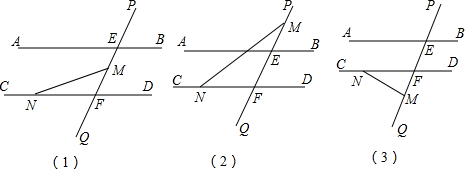
(1)当点M在线段EF上时,如图(1),求证:∠FMN+∠FNM=∠AEF.
(2)当点M在射线EP上时,如图(2),试猜想∠FMN、∠FNM、∠AEF之间的数量关系: (不要求说明理由).
(3)当点M在射线FQ上时,如图(3),试猜想∠FMN、∠FNM、∠AEF之间的数量关系,并说明理由.

(1)当点M在线段EF上时,如图(1),求证:∠FMN+∠FNM=∠AEF.
(2)当点M在射线EP上时,如图(2),试猜想∠FMN、∠FNM、∠AEF之间的数量关系:
(3)当点M在射线FQ上时,如图(3),试猜想∠FMN、∠FNM、∠AEF之间的数量关系,并说明理由.
考点:平行线的性质
专题:
分析:(1)由三角形的内角和定理与平行线的性质,可得∠AEF+∠NFM=180°,∠FMN+∠FNM+∠NFM=180°,继而证得结论;
(2)同(1),由三角形的内角和定理与平行线的性质,可得∠AEF+∠NFM=180°,∠FMN+∠FNM+∠NFM=180°,即可得:∠FMN+∠FNM=∠AEF;
(3)由三角形的内角和定理与平行线的性质,可得∠AEF=∠NFM,∠FMN+∠FNM+∠NFM=180°,继而可求得答案.
(2)同(1),由三角形的内角和定理与平行线的性质,可得∠AEF+∠NFM=180°,∠FMN+∠FNM+∠NFM=180°,即可得:∠FMN+∠FNM=∠AEF;
(3)由三角形的内角和定理与平行线的性质,可得∠AEF=∠NFM,∠FMN+∠FNM+∠NFM=180°,继而可求得答案.
解答:(1)证明:∵AB∥CD,
∴∠AEF+∠NFM=180°,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)关系为:∠FMN+∠FNM=∠AEF.
理由:∵AB∥CD,
∴∠AEF+∠NFM=180°,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM=∠AEF.
(3)数量关系为:∠FMN+∠FNM+∠AEF=180°.
理由:∵AB∥CD,
∴∠AEF=∠NFM,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM+∠AEF=180°.
∴∠AEF+∠NFM=180°,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)关系为:∠FMN+∠FNM=∠AEF.
理由:∵AB∥CD,
∴∠AEF+∠NFM=180°,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM=∠AEF.
(3)数量关系为:∠FMN+∠FNM+∠AEF=180°.
理由:∵AB∥CD,
∴∠AEF=∠NFM,
∵∠FMN+∠FNM+∠NFM=180°,
∴∠FMN+∠FNM+∠AEF=180°.
点评:此题考查了平行线的性质以及三角形内角和定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
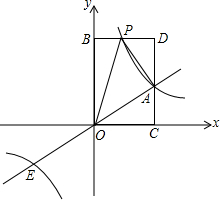 如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
 如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF.
如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF. 如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.
如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.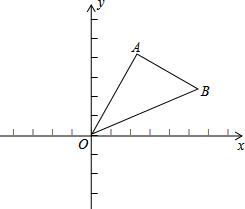 如图,将△AOB在平面直角坐标系中,A,B两点的坐标分别为(2,4)、(6,2),将△AOB沿x轴负方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到△DEF.
如图,将△AOB在平面直角坐标系中,A,B两点的坐标分别为(2,4)、(6,2),将△AOB沿x轴负方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到△DEF.