题目内容
 如图,双曲线y=
如图,双曲线y=| k |
| x |
(1)填空:
①k=
③在每个象限内y随x的增大而
②Q点的坐标为
(2)当m=4,求△POA的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)①根据待定系数法,可得答案;③根据 k的值,可得反比例函数的性质;②根据图象上点的坐标满足函数解析式,可得答案;
(2)根据解方程组,可得P点坐标,根据三角形的面积公式,可得答案.
(2)根据解方程组,可得P点坐标,根据三角形的面积公式,可得答案.
解答:解:(1)①双曲线y=
经过点A (1,4),
k=1×4=4,
③k=4>0,在每个象限内y随x的增大而 而减小;
②Q点的坐标为 (m,
)(含m);
(2)连接AP,作OB⊥AP与B,如图:

当m=4,P(4,1)
OA=OP=
,AP=
=3
,
BP=
,
OB=
=
=
,
S△AOP=
AP•OB=
×
×3
=7.5.
| k |
| x |
k=1×4=4,
③k=4>0,在每个象限内y随x的增大而 而减小;
②Q点的坐标为 (m,
| 4 |
| m |
(2)连接AP,作OB⊥AP与B,如图:

当m=4,P(4,1)
OA=OP=
| 17 |
| (4-1)2+(1-4)2 |
| 2 |
BP=
3
| ||
| 2 |
OB=
| OP2-BP2 |
17-(
|
5
| ||
| 2 |
S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,利用了待定系数法,反比例函数的性质,两点间距离公式,三角形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长为( )
如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长为( )A、2
| ||
B、4
| ||
| C、4 | ||
| D、2 |
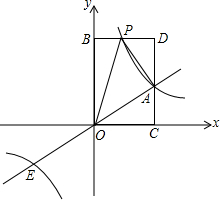 如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
 如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.
如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.