题目内容
临近端午假期,某公司准备组织该公司员工前往溧阳天目湖综合实践基地
进行野外拓展活动.经统计,共有350名员工参加此次活动,行李打包后共有130件.公司计划
租用A、B两种型号的汽车若干辆.经了解,这两种汽车均可同时载人和装行李,这两种汽车的
装载能力如下表所示:
(1)公司至少租用多少辆汽车,能将员工们及他们的行李一次性送达目的地?
(2)若A、B两种汽车每辆的租车费用分别为1000元、850元,请你求出在(1)的条件下
最低租车费用为多少.
进行野外拓展活动.经统计,共有350名员工参加此次活动,行李打包后共有130件.公司计划
租用A、B两种型号的汽车若干辆.经了解,这两种汽车均可同时载人和装行李,这两种汽车的
装载能力如下表所示:
型号 |
每辆汽车的装载能力 | |
| 人数 | 行李数 | |
| A型 | 40 | 10 |
| B型 | 30 | 20 |
(2)若A、B两种汽车每辆的租车费用分别为1000元、850元,请你求出在(1)的条件下
最低租车费用为多少.
考点:一次函数的应用,一元一次不等式的应用
专题:
分析:(1)设该公司至少租用a辆汽车,其中A型汽车x辆,再根据员工人数和行李的件数列出不等式组,求解得到x的取值范围,然后根据x的取值范围列出关于a的不等式,再求解即可;
(2)根据a的值求出x的取值范围,然后列出租车费用的表达式,再根据一次函数的增减性求出最低费用即可.
(2)根据a的值求出x的取值范围,然后列出租车费用的表达式,再根据一次函数的增减性求出最低费用即可.
解答:解:(1)设该公司至少租用a辆汽车,其中A型汽车x辆,
由题意得
,
解不等式①得,x≥35-3a,
解不等式②得,x≤2a-13,
∴35-3a≤x≤2a-13,
∴35-3a≤2a-13,
解得a≥9.6,
∴该公司至少租用10辆汽车;
(2)由(1)知5≤x≤7,
设所租用10辆汽中A型汽车x辆,则B型汽车(10-x)辆,
费用y=1000x+850(10-x),
=150x+8500,
∵150>0,y随x增大而增大,
∴x=5时,y取得最大值,为9250元.
由题意得
|
解不等式①得,x≥35-3a,
解不等式②得,x≤2a-13,
∴35-3a≤x≤2a-13,
∴35-3a≤2a-13,
解得a≥9.6,
∴该公司至少租用10辆汽车;
(2)由(1)知5≤x≤7,
设所租用10辆汽中A型汽车x辆,则B型汽车(10-x)辆,
费用y=1000x+850(10-x),
=150x+8500,
∵150>0,y随x增大而增大,
∴x=5时,y取得最大值,为9250元.
点评:本题考查了一次函数的应用,一元一次不等式的应用,难点在于(1)设两个未知数并列出不等式组,最后求出租车的取值范围,(2)利用一次函数的增减性求最值问题是常用的方法之一,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长为( )
如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长为( )A、2
| ||
B、4
| ||
| C、4 | ||
| D、2 |
 已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D.
已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D.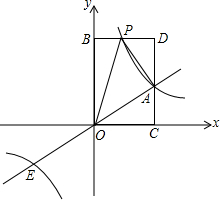 如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数 如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.
如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证:直线AD是⊙O的切线.