题目内容
15.等腰三角形的两边长分别为2和6,则三角形周长为14.分析 根据2和6可分别作等腰三角形的腰,结合三角形三边关系定理,分别讨论求解.
解答 解:当2为腰时,三边为2,2,6,由三角形三边关系定理可知,不能构成三角形;
当6为腰时,三边为6,6,2,符合三角形三边关系定理,周长为:6+6+2=14.
故答案为:14.
点评 本题考查了等腰三角形的性质,三角形三边关系定理.关键是根据2,6分别作为腰,由三边关系定理,分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.当k为何值时,25x2-kxy+49y2是一个完全平方式( )
| A. | -35 | B. | -70 | C. | ±35 | D. | ±70 |
10.下列运算错误的是( )
| A. | (-a)(-a)2=-a3 | B. | -2x2(-3x)=-6x4 | C. | (-a)3(-a)2=-a5 | D. | (-a)3(-a)3=a6 |
7.某车间3月下旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,2,则在这10天中该车间生产的零件的次品数的( )
| A. | 众数是0 | B. | 极差是2 | C. | 平均数是2 | D. | 中位数是2 |
5.正八边形的中心角是( )
| A. | 45° | B. | 135° | C. | 360° | D. | 1080° |
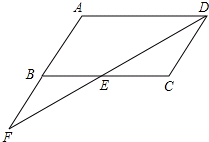 已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.
已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长. 如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.