题目内容
9.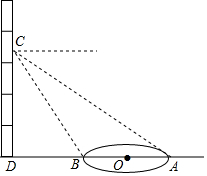 如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)
如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)
分析 先根据题意得出CD的长,利用锐角三角函数的定义得出AD及BD的长,进而可得出结论.
解答 解:∵每层楼高均为3米,测得目高1.5米,
∴CD=3×3+1.5=10.5米.
∵最远点的俯角为30°,
∴∠CAD=30°,
∴tan30°=$\frac{CD}{AD}$,
∴AD=$\frac{3}{\sqrt{3}}$CD=$\sqrt{3}$CD.
∵∠CBD=60°,
∴tan60°=$\frac{CD}{BD}$,
∴BD=$\frac{1}{\sqrt{3}}$CD=$\frac{\sqrt{3}}{3}$CD,
∴AB=AD-BD=($\sqrt{3}$-$\frac{\sqrt{3}}{3}$)×10.5=7$\sqrt{3}$,
∴S=($\frac{7\sqrt{3}}{2}$)2π≈115.4(平方米).
答:圆形花园的面积是115.4平方米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  等边三角形 | B. |  正方形 | C. |  平行四边形 | D. |  正五边形 |
1.下列运算正确的是( )
| A. | (-a3)2=a6 | B. | xp•yp=(xy)2p | C. | x6÷x3=x2 | D. | (m+n)2=m2+n2 |
19.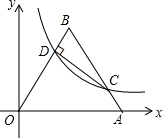 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )| A. | $\frac{9}{16}$$\sqrt{3}$ | B. | $\frac{3}{4}$$\sqrt{3}$ | C. | $\frac{9}{25}$$\sqrt{3}$ | D. | $\frac{3}{5}$$\sqrt{3}$ |
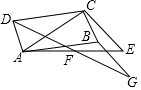 如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.
如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.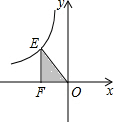 位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )
位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )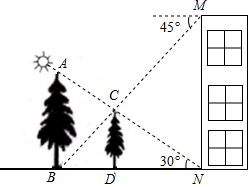 如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)
如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)