题目内容
19.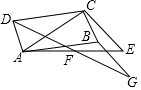 如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.
如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.(1)猜想BG与CE的关系,并证明你的猜想;
(2)求证:BG⊥AC.
分析 (1)结论:BG=CE,BG∥CE.连接AG、DF、EG.易证四边形ADEG是平行四边形,推出AD=EG,AD∥EG,由四边形ABCD是平行四边形,推出AD∥BC,AD=BC,推出BC=EG,BC∥EG,推出四边形BCEG是平行四边形,即可解决问题;
(2)由四边形BCEG是平行四边形,推出BG∥EC,由CE⊥AC,即可推出BG⊥AC;
解答 (1)解:结论:BG=CE,BG∥CE.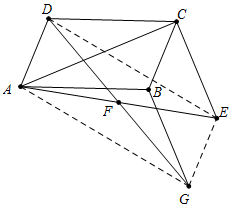
理由:连接AG、DF、EG.
∵DF=FG,AF=FE,
∴四边形ADEG是平行四边形,
∴AD=EG,AD∥EG,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴BC=EG,BC∥EG,
∴四边形BCEG是平行四边形,
∴BG=CE,BG∥CE.
(2)证明:∵四边形BCEG是平行四边形,
∴BG∥EC,
∵CE⊥AC,
∴BG⊥AC.
点评 本题考查平行四边形的判定和性质、两直线的位置关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若二次根式$\sqrt{3x-2}$有意义,则x的取值范围是( )
| A. | x≥$\frac{2}{3}$ | B. | x≤$\frac{2}{3}$ | C. | x≥$\frac{3}{2}$ | D. | x≤$\frac{3}{2}$ |
2.定义新运算“⊕”如下:当a>b时,a⊕b=ab+b;当a<b时,a⊕b=ab-b,若3⊕(x+2)>0,则x的取值范围是( )
| A. | -1<x<1或x<-2 | B. | x<-2或1<x<2 | C. | -2<x<1或x>1 | D. | x<-2或x>2 |
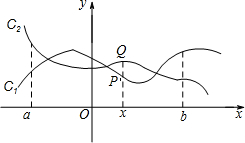 如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.
如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.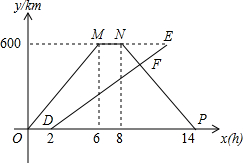 A、B两地相距600km,甲、乙两车都从A地出发,沿着同一路线匀速驶向B地,乙车比甲车晚出发2h,甲车到达B地停留2h立即按原路匀速返回,图中折线OMNP和线段DE分别是两车离A地的距离y(km)与甲车行驶时间x(h)之间的函数图象.
A、B两地相距600km,甲、乙两车都从A地出发,沿着同一路线匀速驶向B地,乙车比甲车晚出发2h,甲车到达B地停留2h立即按原路匀速返回,图中折线OMNP和线段DE分别是两车离A地的距离y(km)与甲车行驶时间x(h)之间的函数图象.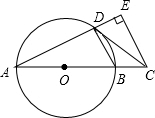 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.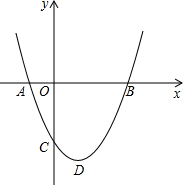 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中: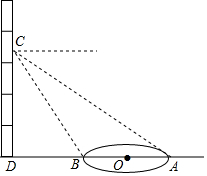 如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)
如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)