题目内容
等腰梯形的各边都与⊙O相切，⊙O的直径为8cm，梯形的腰长为10cm，则等腰梯形的上底长为 cm．
考点：切线长定理
专题：
分析：利用等腰三角形的性质结合切线长定理得出AD+BC=AB+DC，即可求出．
解答：
解：如图所示：过点A作AF⊥BC于点F，DE⊥BC与点E，
∵等腰梯形的各边都与⊙O相切，⊙O的直径为8cm，梯形的腰长为10cm，
∴DE=8cm，DC=10cm，
则EC=6cm，
故BF=6cm，
故AD+BF+EC+EF=20，
则2AD+12=20，
解得：AD=4．
故答案为：4．
解：如图所示：过点A作AF⊥BC于点F，DE⊥BC与点E，∵等腰梯形的各边都与⊙O相切，⊙O的直径为8cm，梯形的腰长为10cm，
∴DE=8cm，DC=10cm，
则EC=6cm，
故BF=6cm，
故AD+BF+EC+EF=20，
则2AD+12=20，
解得：AD=4．
故答案为：4．
点评：此题主要考查了切线长定理以及勾股定理等知识，得出BF=EC=6cm是解题关键．
练习册系列答案
相关题目
已知m2+2mn=13，3mn+2n2=21，则2m2+13mn+6n2-44的值为（ ）
| A、45 | B、5 | C、66 | D、77 |
从长为3，6，7，9的4条线段中任取3条作三角形的边，能组成三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上，AB=3，BC=5，tan∠AFB=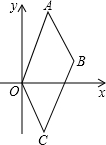
如图，在平面直角坐标系中，A（1，3）、B（2，1），四边形ABCD是平行四边形，求点C的坐标．
如图，在Rt△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，且∠EDF=45°，求证：AE+EF=FC．四点整，时钟的时针与分针之间的夹角是（ ）
| A、60° | B、90° |
| C、120° | D、150° |
如图所示，CE是△ABC的外角∠ACF的平分线，CE交BA的延长线于点E，则∠BAC与∠B谁大？并说明理由．