题目内容
 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,且∠EDF=45°,求证:AE+EF=FC.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,且∠EDF=45°,求证:AE+EF=FC.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:连接AD,在CA上找到点G使得CG=AE,易证△ADE≌△CDG,可得∠ADE=∠CDG,DE=DG,AE=CG,即可求得∠FDG=45°,即可证明△EDF≌△GDF,可得EF=FG,即可解题.
解答:证明:连接AD,在CA上找到点G使得CG=AE,

∵AB=AC,∠BAC=90°,
∴∠BAD=∠C=45°,AD=BD=CD,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴∠ADE=∠CDG,DE=DG,AE=CG,
∵∠ADE+∠ADF=90°,
∴∠ADF+∠CDG=90°,
∴∠FDG=45°,
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS),
∴EF=FG,
∵FC=FG+CG,
∴FC=EF+AE.

∵AB=AC,∠BAC=90°,
∴∠BAD=∠C=45°,AD=BD=CD,
在△ADE和△CDG中,
|
∴△ADE≌△CDG(SAS),
∴∠ADE=∠CDG,DE=DG,AE=CG,
∵∠ADE+∠ADF=90°,
∴∠ADF+∠CDG=90°,
∴∠FDG=45°,
在△EDF和△GDF中,
|
∴△EDF≌△GDF(SAS),
∴EF=FG,
∵FC=FG+CG,
∴FC=EF+AE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ADE≌△CDG和△EDF≌△GDF是解题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
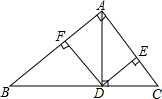 如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( ) 如图,AB是⊙O的直径,D是
如图,AB是⊙O的直径,D是
 如图,正三角形ABC的边长为2,点A,B在半径为
如图,正三角形ABC的边长为2,点A,B在半径为