题目内容
11.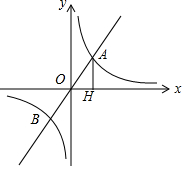 已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.
已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.(1)求这两个函数的解析式;
(2)如果△OAC是以OA为腰的等腰三角形,且点C在x轴上,求点C的坐标.
分析 (1)根据点A的横坐标可得出OH的长度,从而结合△AOH的面积可得出AH的长度;从而得出点A的坐标,将点A的坐标代入正比例函数及反比例函数解析式,可得出两个函数的解析式;
(2)分两种情况讨论,①OA=OC,②OA=AC,分别求出点C的坐标即可.
解答 解:(1)∵点A的横坐标为1,AH⊥x轴,
∴OH=1,
∵S△AOH=1,
∴$\frac{1}{2}$OH×AH=1,
解得:AH=2.
∴点A的坐标为A(1,2),
∵点A(1,2)在正比例函数y=k1x的图象上,
∴2=k1•1,
解得:k1=2.
∴所求的正比例函数的解析式为y=2x,
∵点A(1,2)在反比例函数$y=\frac{k_2}{x}$的图象上,
∴2=$\frac{{k}_{2}}{1}$,
解得k2=2.
∴所求的反比例函数的解析式为y=$\frac{2}{x}$.
(2)由题意,设点C的坐标为(a,0).
∵△OAC是以OA为腰的等腰三角形,
∴OA=OC或OA=AC,
①当OA=OC时,a=±$\sqrt{5}$,
即可得:点C的坐标为($\sqrt{5}$,0)或(-$\sqrt{5}$,0).
②当OA=AC时,a=2;a=0,
∵点C与点O不重合,
∴a=0不合题意舍去,
∴点C的坐标为(2,0),
综上所述:点C的坐标为($\sqrt{5}$,0)或(-$\sqrt{5}$,0)或(2,0).
点评 本题属于反比例函数综合题,涉及了待定系数法求函数解析式等腰三角形的性质,综合性较强,难点在第三问,注意分类讨论,不要漏解.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
1.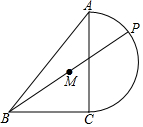 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |
3.古代有这样一个寓言故事:驴子和骡子一同走,它们驮着不同袋数的货物,每袋货物都是一样重的.驴子抱怨负担太重,骡子说:“你抱怨干嘛,如果你给我一袋,那我所负担的就是你的两倍;如果我给你一袋,我们才恰好驮的一样多!”如果设驴子驮的袋数为x袋,骡子驮的袋数为y袋,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{y+1}{2}=(x-1)}\\{y+1=x-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+1=\frac{1}{2}(x-1)}\\{y-1=x+1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y-1=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y+1=x-1}\end{array}\right.$ |
20.点(-1,y1)、(-2,y2)、(3,y3)均在y=-$\frac{6}{x}$的图象上,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y3<y1<y2 |
