题目内容
4．方程组$\left\{\begin{array}{l}x+y=5\\ x+z=3\\ y+z=4\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$．分析 由①+②+③可得x+y+z=6，再分别与方程①、②、③相减可求得答案．
解答 解：
在方程组$\left\{\begin{array}{l}{x+y=5①}\\{x+z=3②}\\{y+z=4③}\end{array}\right.$中
①+②+③可得2（x+y+z）=12，
∴x+y+z=6④，
④-①可得z=1，
④-②可得y=3，
④-③可得x=2，
∴原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$．
故答案为：$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$．
点评 本题主要考查三元一次方程组的解法，解方程组即“转化”，化高次为低次，注意消元的方法．
练习册系列答案
相关题目
14．
有理数a，b在数轴上对应的点的位置如图所示，下列结论成立的是（ ）
有理数a，b在数轴上对应的点的位置如图所示，下列结论成立的是（ ）| A． | a+b＞0 | B． | a+b=0 | C． | a+b＜0 | D． | a-b＞0 |
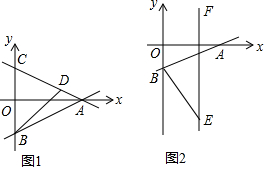已知直线l1：y=$\frac{1}{2}$x-2与x轴交于点A，与y轴交于点B，将直线沿x轴翻折，得到一个新函数的图象l2（图1），直线l2与y轴交于点C．