题目内容
3.下列说法中,不正确的是( )| A. | 5是25的算术平方根 | B. | m2n与mn2是同类项 | ||
| C. | 多项式-3a3b+7ab+1的次数是4 | D. | -8的立方根为-2 |
分析 分别利用算术平方根以及多项式的次数、同类项的定义、立方根的定义分别分析得出答案.
解答 解:A、5是25的算术平方根,正确,不合题意;
B、m2n与mn2不是同类项,故此选项错误,符合题意;
C、多项式-3a3b+7ab+1的次数是4,正确,不合题意;
D、-8的立方根为-2,正确,不合题意.
故选:B.
点评 此题主要考查了算术平方根以及多项式的次数、同类项的定义、立方根的定义等知识,正确掌握相关定义是解题关键.

练习册系列答案
相关题目
13. 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )| A. | 720° | B. | 540° | C. | 360° | D. | 180° |
14.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查我市初中学生每天锻炼身体的平均时间 | |
| B. | 调查某校初三(五)班学生的平均体重 | |
| C. | 调查某街道90岁以上老人的健康情况 | |
| D. | 调查某中学高一(一)班学生的课外阅读情况 |
18.云南某县境内发生地震,某市积极筹集救灾物资260吨从该市区运往该县甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 车 型 运往地 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
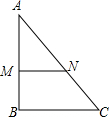 如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( )
如图,在△ABC中,AC=10,AB=8,直线l分别与AB,AC交于M,N两点,且l∥BC,若S△AMN:S△ABC=4:9,则AM+AN的长为( ) 请你根据王老师所给的内容,完成下列各小题.
请你根据王老师所给的内容,完成下列各小题. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则△EFG与△BCG面积之比是$\frac{1}{16}$.
如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则△EFG与△BCG面积之比是$\frac{1}{16}$.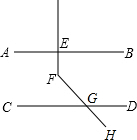 如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.
如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.