题目内容
已知关于x的一元二次方程x2+cx+a=0的两个整数根恰好比方程x2+ax+b=0的两个根都大1,求a+b+c的值.
( )
( )
| A、29 | B、-3或29 |
| C、-3 | D、26 |
考点:根与系数的关系
专题:
分析:设出第一个方程的两根,表示出后面方程的另2根,利用根与系数的关系均得到与a的关系,进而消去a,得到两个一次项的积为一个常数的形式,判断可能的整数解,得到a,b,c的值,相加即可.
解答:解:设方程x2+ax+b=0的两个根为α,β,
∵方程有整数根,
设其中α,β为整数,且α≤β,
则方程x2+cx+a=0的两根为α+1,β+1,
∴α+β=-a,(α+1)(β+1)=a,
两式相加,得αβ+2α+2β+1=0,
即(α+2)(β+2)=3,
∴
或
,
解得
或
,
又∵a=-(α+β)=-[(-1)+1]=0,b=αβ=-1×1=-1,c=-[(α+1)+(β+1)]=-[(-1+1)+(1+1)]=-2,
或a=-(α+β)=-[(-5)+(-3)]=8,b=αβ=(-5)×(-3)=15,c=-[(α+1)+(β+1)]=-[(-5+1)+(-3+1)]=6,
∴a=0,b=-1,c=-2或者a=8,b=15,c=6,
∴a+b+c=0+(-1)+(-2)=-3或a+b+c=8+15+6=29,
故a+b+c=-3或29,
故选:B..
∵方程有整数根,
设其中α,β为整数,且α≤β,
则方程x2+cx+a=0的两根为α+1,β+1,
∴α+β=-a,(α+1)(β+1)=a,
两式相加,得αβ+2α+2β+1=0,
即(α+2)(β+2)=3,
∴
|
|
解得
|
|
又∵a=-(α+β)=-[(-1)+1]=0,b=αβ=-1×1=-1,c=-[(α+1)+(β+1)]=-[(-1+1)+(1+1)]=-2,
或a=-(α+β)=-[(-5)+(-3)]=8,b=αβ=(-5)×(-3)=15,c=-[(α+1)+(β+1)]=-[(-5+1)+(-3+1)]=6,
∴a=0,b=-1,c=-2或者a=8,b=15,c=6,
∴a+b+c=0+(-1)+(-2)=-3或a+b+c=8+15+6=29,
故a+b+c=-3或29,
故选:B..
点评:主要考查一元二次方程根与系数关系的应用;利用根与系数的关系得到两根之间的关系是解决本题的关键;消去a后得到两个一次项的积为一个常数的形式是解决本题的难点.

练习册系列答案
相关题目
对于正数x,规定 f(x)=
,例如:f(4)=
=
,f(
)=
=
,则f(2013)+f(2012)+…+f(2)+f(1)+f(
)+f(
)+…+f(
)的值为( )
| 1 |
| 1+x |
| 1 |
| 1+4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 | ||
1+
|
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| A、2012 |
| B、2012.5 |
| C、2013 |
| D、2013.5 |
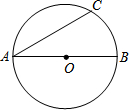 如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为( )
如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为( )| A、30° |
| B、60° |
| C、60°或90° |
| D、30°或90° |
在边长为a的正方形内取一点,使这点到一边上的两个顶点与到对边的距离相等,则这一距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在直角坐标系中,O为坐标原点A(1,3),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有( )
| A、4个 | B、3个 | C、2个 | D、5个 |
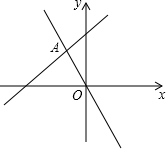 如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )
如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )A、x>
| ||
| B、x<m | ||
| C、x>m | ||
D、x>-
|