题目内容
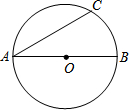 如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为( )
如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为( )| A、30° |
| B、60° |
| C、60°或90° |
| D、30°或90° |
考点:圆周角定理
专题:计算题
分析:分类讨论:当AD与AC在直径AB的两旁,连结OD,由于AB=2,AD=1,AD=OD=OA,于是可判断△OAD为等边三角形,根据等边三角形的性质得∠OAD=60°,再利用∠CAD=∠CAB+∠OAD进行计算;当AD与AC在直径AB的同旁,则利用∠CAD=∠OAD-∠CAB求解.
解答: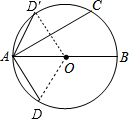 解:如图,
解:如图,
当AD与AC在直径AB的两旁,连结OD,
∵AB=2,AD=1,
∴AD=OD=OA,
∴△OAD为等边三角形,
∴∠OAD=60°,
∴∠CAD=∠CAB+∠OAD=30°+60°=90°;
当AD与AC在直径AB的同旁,则∠CAD=∠OAD-∠CAB=60°-30°=30°.
综上所述,∠CAD的度数为30°或90°.
故选D.
 解:如图,
解:如图,当AD与AC在直径AB的两旁,连结OD,
∵AB=2,AD=1,
∴AD=OD=OA,
∴△OAD为等边三角形,
∴∠OAD=60°,
∴∠CAD=∠CAB+∠OAD=30°+60°=90°;
当AD与AC在直径AB的同旁,则∠CAD=∠OAD-∠CAB=60°-30°=30°.
综上所述,∠CAD的度数为30°或90°.
故选D.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期,收获时,从中任选并摘了10棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
用你所学的知识估计今年此果园樱桃的总产量约为( )
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 质量(kg) | 14 | 21 | 27 | 17 | 18 | 20 | 19 | 23 | 19 | 22 |
| A、200kg |
| B、1900kg |
| C、2000kg |
| D、1850kg |
下列名人中:①比尔•盖茨;②高斯;③袁隆平;④诺贝尔;⑤陈景润;⑥华罗庚;⑦高尔基;⑧爱因斯坦,其中是数学家的是( )
| A、①④⑦ | B、③④⑧ |
| C、②⑥⑧ | D、②⑤⑥ |
已知关于x的一元二次方程x2+cx+a=0的两个整数根恰好比方程x2+ax+b=0的两个根都大1,求a+b+c的值.
( )
( )
| A、29 | B、-3或29 |
| C、-3 | D、26 |
 已知⊙O的半径是1,△ABC内接于圆O.若∠B=34°,∠C=110°,则弧BC的长为( )
已知⊙O的半径是1,△ABC内接于圆O.若∠B=34°,∠C=110°,则弧BC的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
小红做四次抛投硬币的试验,前三次都是正面向上,那么她第四次抛投硬币时正面向上的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |