题目内容
 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°(1)求证:BD=CE;
(2)求证:BD⊥CE.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)由三角形ABC与三角形ADE都为等腰直角三角形,利用等腰三角形的性质得到两边及夹角相等,利用SAS可得出三角形ABD与三角形ACE全等,利用全等三角形的对应边相等即可得证;
(2)延长CE到F,交BD于点F,利用全等三角形对应角相等得到∠ACE=∠ABD,利用等腰三角形的两锐角为45°,等量代换得到CF垂直于BD,得证.
(2)延长CE到F,交BD于点F,利用全等三角形对应角相等得到∠ACE=∠ABD,利用等腰三角形的两锐角为45°,等量代换得到CF垂直于BD,得证.
解答: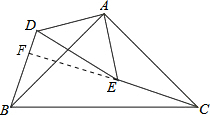 证明:(1)∵△ABC与△ADE都为等腰直角三角形,
证明:(1)∵△ABC与△ADE都为等腰直角三角形,
∴∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC-∠BAE=∠DAE-∠BAE,即∠DAB=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)延长CE,交BD于点F,
∵△ABD≌△ACE,
∴∠ACE=∠ABD,
∵∠ACE+∠BCE=45°,
∴∠ABD+∠BCE=45°,
∴∠FBC+∠BCF=∠ABC+∠ABD+∠BCF=90°,
∴∠BFC=90°,
则CF⊥BD,即BD⊥CE.
 证明:(1)∵△ABC与△ADE都为等腰直角三角形,
证明:(1)∵△ABC与△ADE都为等腰直角三角形,∴∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC-∠BAE=∠DAE-∠BAE,即∠DAB=∠EAC,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)延长CE,交BD于点F,
∵△ABD≌△ACE,
∴∠ACE=∠ABD,
∵∠ACE+∠BCE=45°,
∴∠ABD+∠BCE=45°,
∴∠FBC+∠BCF=∠ABC+∠ABD+∠BCF=90°,
∴∠BFC=90°,
则CF⊥BD,即BD⊥CE.
点评:此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列各式中不能用平方差公式计算的是( )
| A、(-x+y)(-x-y) |
| B、(a-2b)(2b+a) |
| C、(a-b)(a+b)(a2+b2) |
| D、(a+b-c)(a+b-c) |

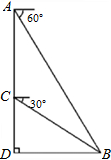 小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)