题目内容
已知a、b为自然数,且a+b=40.
(1)求a2+b2的最小值;
(2)求ab的最大值.
(1)求a2+b2的最小值;
(2)求ab的最大值.
考点:二次函数的最值
专题:
分析:(1)先根据a、b为自然数,且a+b=40得出a=40-b,再根据二次函数的性质即可得出结论;
(2)根据(1)中a2+b2的最小值即可得出结论.
(2)根据(1)中a2+b2的最小值即可得出结论.
解答:解:(1)∵a、b为自然数,且a+b=40,
∴a=40-b,
∴a2+b2=(40-b)2+b2=2b2-80b+1600,
∴a2+b2最小=
=800;
(2)∵由(1)知,a2+b2最小值为800,a2+b2≥2ab,
∴ab的最大值=
=
=400.
∴a=40-b,
∴a2+b2=(40-b)2+b2=2b2-80b+1600,
∴a2+b2最小=
| 4×2×1600-(-80)2 |
| 4×2 |
(2)∵由(1)知,a2+b2最小值为800,a2+b2≥2ab,
∴ab的最大值=
| a2+b2 |
| 2 |
| 800 |
| 2 |
点评:本题考查的是二次函数的最值,熟知二次函数y=ax2+bx+c(a>0)中,当x=-
时,y最小=
是解答此题的关键.
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若关于x的一元二次方程ax2+bx+c=0(a≠0)中有a-b+c=0,则该方程中必有一根是( )
| A、0 | B、1 | C、-1 | D、±1 |
 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90° 如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点.
如图,抛物线y=-x2+2x+3与x轴分别交于A、B两点. 矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm
矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm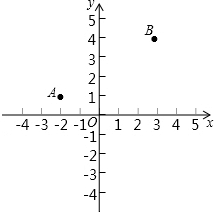 如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4).
如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4).