题目内容
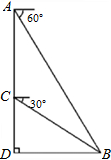 小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:在Rt△BCD中和Rt△ABD中分别用CD表示出AD和BD的长度,然后根据
=tan60°,代入求成CD的长度,然后求出BD的长度.
| AD |
| BD |
解答:解:在Rt△BCD中,
∵∠BCD=90°-30°=60°,
∴
=tan60°,
则BD=
CD,
在Rt△ABD中,
∵∠ABD=60°,
∴
=tan60°,
即
=
,
解得:CD=20(米),
∴BD=
CD=20
≈35(米).
答:BD之间的直线距离约为35米.
∵∠BCD=90°-30°=60°,
∴
| BD |
| CD |
则BD=
| 3 |
在Rt△ABD中,
∵∠ABD=60°,
∴
| AD |
| BD |
即
| 40+CD | ||
|
| 3 |
解得:CD=20(米),
∴BD=
| 3 |
| 3 |
答:BD之间的直线距离约为35米.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90° 矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm
矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm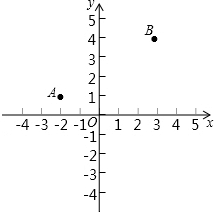 如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4).
如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4). 如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.
如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.