题目内容
图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它平均分成形状和大小都一样的四块小长方形,然后按图②那样拼成一个正方形.

(1)观察图②,请用两种不同的方法表示图②中阴影部分的面积:方法1: ;方法2: ;
(2)直接写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求a-b的值.

(1)观察图②,请用两种不同的方法表示图②中阴影部分的面积:方法1:
(2)直接写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求a-b的值.
考点:完全平方公式的几何背景
专题:
分析:(1)利用正方形的面积公式以及大正方形的面积减去四个矩形的面积就是阴影部分的面积就可以列式求解;
(2)根据两种表示法都是表示阴影部分的面积,则二者相等,即可求解;
(3)利用(2)的结论即可求解.
(2)根据两种表示法都是表示阴影部分的面积,则二者相等,即可求解;
(3)利用(2)的结论即可求解.
解答:解:(1)方法1:(m-n)2;方法2:(m+n)2-4mn;
(2)(m+n)2,(m-n)2,mn之间的等量关系:(m-n)2=(m+n)2-4mn;
(3)∵(a-b)2=(a+b)2-4ab=49-20=29,
∴a-b=±
.
(2)(m+n)2,(m-n)2,mn之间的等量关系:(m-n)2=(m+n)2-4mn;
(3)∵(a-b)2=(a+b)2-4ab=49-20=29,
∴a-b=±
| 29 |
点评:本题考查对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
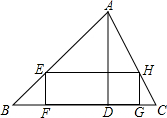 如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.
如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米. 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90° 矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm
矩形的周长是16cm,设矩形的一边长为xcm,另一边长为ycm