如图.AD∥BC.AD=CB.AE=CF.求证:BE∥DF．题目和参考答案——青夏教育精英家教网—

题目内容

4．

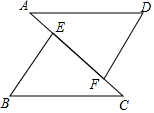如图，AD∥BC，AD=CB，AE=CF，求证：BE∥DF．

分析要证BE∥DF，可先证∠BEC=∠AFD，因为∠BEC和∠AFD在图中是△ADF和△CBE的对应角，所以根据已知条件得出△ADF≌△CBE，即可证明．

解答 19．证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AF=AE+EF=CF+EF=CE，
在△ADF和△CBE中，$\left\{\begin{array}{l}{AF=CE}\\{∠A=∠C}\\{AD=BC}\end{array}\right.$
∴△ADF≌△CBE，
∴∠AFD=∠CEB，
∴BE∥DF．

点评此题是全等三角形的判定和性质；三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，涉及到等式的性质，平行线的性质和判定，解本题的关键是判断出AF=CE，属于基础题型．

练习册系列答案

相关题目

14．

如图，点C在线段AB上，AC=6cm，MB=10cm，点M，N分别为AC，BC的中点．
（1）求线段BC，MN的长；
（2）若C在线段AB的延长线上，且满足AC-BC=acm，M，N分别是线段AC，BC的中点，请画出图形，并用a的式子表示MN的长度．

15．

已知某四棱柱的俯视图如图所示，画出它的主视图和左视图．

12．如图所示，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以发现终点表示的数是-2，已知点A，B是数轴上的点，请参照图并思考，完成下列各题．

（1）如果点A表示数-3，将点A向右移动7个单位长度，那么终点B表示的数是4，A、B两点间的距离是7；
（2）如果点A表示数3，将点A向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是1，A、B两点间的距离为2；
（3）如果点A表示数-4，将点A向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是-92，A、B两点间的距离为88．
（4）一般地，如果A点表示的数为m，将A点向右移动n个单位长度，再向左移动p个单位长度，那么，请你猜想终点B表示的数是m+n-p，A、B两点间的距离是|n-p|．

19．（1）解方程：$\frac{1}{x-2}$-3=$\frac{x-1}{2-x}$；
（2）已知4x=3y，求代数式（x-2y）²-（x-y）（x+y）-2y²的值．

9．

如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°．
（1）求证：AC是⊙O的切线；
（2）求图中阴影部分的面积．

16．

如图所示，C，D是线段AB上的两点，AC=$\frac{5}{9}$BC，AD=$\frac{9}{5}$DB，若CD=2cm，求线段AB的长．

13．解下列方程组：
（1）$\left\{\begin{array}{l}{2x+y=3}\\{x-y=0}\end{array}\right.$
（2）$\left\{\begin{array}{l}{x+3y=12}\\{2x-3y=6}\end{array}\right.$
（3）$\left\{\begin{array}{l}{3x-y=4}\\{3x+y=14}\end{array}\right.$
（4）$\left\{\begin{array}{l}{x+y=6}\\{y+2x=2}\end{array}\right.$．

20．火车票上的车次号有两个意义：一是数字越小表示车速越快，1-98次为特快列车，101-198次为直快列车，301-398次为普快列车，401-498次为普客列车；二是单数与双数表示不同的行驶方向，其中单数表示从南京开出，双数表示开往南京．根据以上信息，上海开往南京的某一直快列车的车次号可能是（　　）

试题分类