题目内容
9.已知关于x的一元二次方程x2+kx-3=0.(1)当k=2时,原一元二次方程的解是x1=-3,x2=1;
(2)求证:不论k为何实数,方程总有两个不相等的实数根.
分析 (1)把k=2代入原方程,利用因式分解法解方程即可;
(2)先求出方程的根的判别式△=k2-4×1×(-3)=k2+12,利用非负数的性质即可证明.
解答 解:(1)当k=2时,x2+2x-3=0,
∴(x+3)(x-1)=0,
∴x+3=0或x-1=0,
∴x1=-3,x2=1;
(2)∵一元二次方程x2+kx-3=0得判别式△=k2-4×1×(-3)=k2+12,
又∵不论k为何实数,k2≥0,
∴k2+12≥12>0,
∴△>0,
∴不论k为何实数,原方程总有两个不相等的实数根.
点评 本题主要考查了根的判别式以及因式分解法解一元二次方程的知识,解答本题的关键是熟练掌握△>0?方程有两个不相等的实数根,此题难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.要使(-6x3)(x2+ax+5)+3x4的结果中不含x4项,则a的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
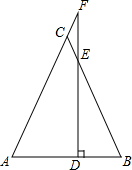 如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.
如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.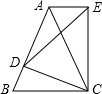 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为底边,向上作等腰△DCE,使△EDC∽△ABC,连接AE.
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为底边,向上作等腰△DCE,使△EDC∽△ABC,连接AE. 如图,等腰直角三角形ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D,E,求图中阴影部分的面积.
如图,等腰直角三角形ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D,E,求图中阴影部分的面积.