题目内容
20.若|x-1|+(xy-2)2=0,求:$\frac{1}{xy}+\frac{1}{(x+1)(y+1)}+\frac{1}{(x+2)(y+2)}+$…$+\frac{1}{(x+2006)(y+2006)}$的值.分析 先由非负数的性质求得x=1,y=2,然后将x、y的值代入,最后利用拆项裂项法求解即可.
解答 解:∵|x-1|+(xy-2)2=0,
∴x=1,y=2.
将x=1,y=2代入得:原式=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$+…+$\frac{1}{2007×2008}$
=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{2007}-\frac{1}{2008}$
=1-$\frac{1}{2008}$
=$\frac{2007}{2008}$.
点评 本题主要考查的是非负数的性质,求代数式的值,利用利用拆项裂项法求得算式的值是解题的关键.

练习册系列答案
相关题目
11.函数y=x2+x-6的图象与y轴交点的纵坐标是( )
| A. | -4 | B. | -4 | C. | 0 | D. | -6 |
8.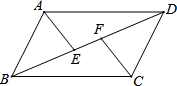 如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
 如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )
如图,AB=CD,AB∥CD,E,F是BD上两点且BE=DF,则图中全等的三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
10.下列方程的解是x=2的是( )
| A. | 3x+2x=-2 | B. | 3x-2x=-2 | C. | 3x+2x=2 | D. | 3x-2x=2 |
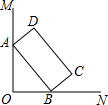 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.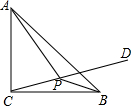 如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )