题目内容
4.要使(-6x3)(x2+ax+5)+3x4的结果中不含x4项,则a的值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
分析 根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加,可得多项式,根据四次项的系数为零,可得答案.
解答 解:原式=-6x5-6ax4-30x3+3x4
=-6x5+(3-6a)x4-30x3,
(-6x3)(x2+ax+5)+3x4的结果中不含x4项,得
3-6a=0.
解得a=$\frac{1}{2}$,
故选:B.
点评 本题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.

练习册系列答案
相关题目

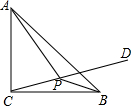 如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( )
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|PA-PB|的最大值是( ) 如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.
如图,AB、CD相交于点E,EA=EC,AC∥BD.求证:EB=ED.