题目内容

18．三角形两边的长分别是4和3，第三边的长是一元二次方程x2-6x+5=0的一个实数根，则该三角形的周长是（　　）
A．8B．10C．12D．8或12

分析 方程利用因式分解法求出解得到第三边，即可确定出周长．

解答 解：方程x2-6x+5=0，
分解因式得：（x-1）（x-5）=0，
解得：x=1或x=5，
若x=1，可得1+3=4，不能构成三角形，舍去；
若x=5，则有3，4，5，能构成三角形，此时周长为3+4+5=12，
故选C．

点评 此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．

练习册系列答案
相关题目
8．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（　　）
A．34°B．56°C．66°D．54°
9．计算：
（1）$-\frac{1}{3}+（-5）-\frac{8}{3}$；
（2）$（\frac{1}{2}-\frac{2}{3}+\frac{1}{6}）×（-12）$．
6．如图，△ABC是等边三角形．
（1）作△ABC的外接⊙O（用尺规作图，保留作图痕迹，不写作法）；
（2）若AB=6cm，求⊙O的半径．
13．已知二次函数y=x2-6x+5．
（1）将y=x2-6x+5化成y=a（x-h）2+k的形式；
（2）求该二次函数的图象的对称轴和顶点坐标；
（3）当x取何值时，y随x的增大而减小．
3．一列火车匀速行驶，经过一条长300米的隧道需要20秒的时间．隧道的顶上有一盏灯，垂直向下发光，灯光照在火车上的时间是10秒．求这列火车的长度．
小冉根据学习解决应用问题的经验对上面问题进行了探究，下面是小冉的探究过程，请补充完成：
设这列火车的长度是x米，那么
（1）从车头经过灯下到车尾经过灯下，火车所走的路程是x米，这段时间内火车的平均速度是$\frac{x}{10}$米/秒；
（2）从车头进入隧道到车尾离开隧道，火车所走的路程是（x+300）米，这段时间内火车的平均速度是$\frac{x+300}{20}$米/秒；
（3）火车经过灯下和火车通过隧道的平均速度的关系是相等；
（4）由此可以列出方程并求解出这列火车的长度（请列方程求解）
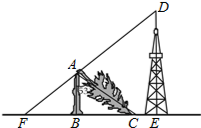10．如图，一棵大树在一次强台风中折断倒下，未折断树杆AB与地面仍保持垂直的关系，而折断部分AC与未折断树杆AB形成53°的夹角．树杆AB旁有一座与地面垂直的铁塔DE，测得BE=6米，塔高DE=9米．在某一时刻的太阳照射下，未折断树杆AB落在地面的影子FB长为4米，且点F、B、C、E在同一条直线上，点F、A、D也在同一条直线上．求这棵大树没有折断前的高度．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.33）
7．先化简，再求值：$\frac{1}{2}$x-（2x-$\frac{2}{3}$y2+3xy）+（$\frac{3}{2}$x-x2+$\frac{1}{3}$y2）+2xy，其中x=-2，y=$\frac{1}{2}$．
5．不等式$\left\{\begin{array}{l}{x≥-3}\\{x＞a}\end{array}\right.$ 的解为x≥-3，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网