题目内容
13.已知二次函数y=x2-6x+5.(1)将y=x2-6x+5化成y=a(x-h)2+k的形式;
(2)求该二次函数的图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而减小.
分析 (1)运用配方法把一般式化为顶点式;
(2)根据二次函数的性质解答即可;
(3)根据二次函数的开口方向和对称轴解答即可.
解答 解:(1)y=x2-6x+5=(x-3)2-4;
(2)二次函数的图象的对称轴是x=3,顶点坐标是(3,-4);
(3)∵抛物线的开口向上,对称轴是x=3,
∴当x≤3时,y随x的增大而减小.
点评 本题考查的是二次函数的三种形式和二次函数的性质,灵活运用配方法把一般式化为顶点式是解题的关键,注意二次函数的性质的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.三角形两边的长分别是4和3,第三边的长是一元二次方程x2-6x+5=0的一个实数根,则该三角形的周长是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 8或12 |
5.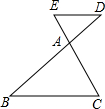 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )| A. | BD:AB=CE:AC | B. | DE:BC=AB:AD | C. | AB:AC=AD:AE | D. | AD:DB=AE:EC |
2.将-$\frac{3}{4}$,-$\frac{5}{6}$,-$\frac{7}{8}$按从小到大的顺序排列( )
| A. | -$\frac{7}{8}$<-$\frac{5}{6}$<-$\frac{3}{4}$ | B. | -$\frac{7}{8}$<-$\frac{3}{4}$<-$\frac{5}{6}$ | C. | -$\frac{5}{6}$<-$\frac{7}{8}$<-$\frac{3}{4}$ | D. | -$\frac{3}{4}$<-$\frac{5}{6}$<-$\frac{7}{8}$ |


