题目内容
6. 如图,△ABC是等边三角形.
如图,△ABC是等边三角形.(1)作△ABC的外接⊙O(用尺规作图,保留作图痕迹,不写作法);
(2)若AB=6cm,求⊙O的半径.
分析 (1)直接利用外接圆的作法作出三角形任意两边的垂直平分线,进而得出外接圆圆心,进而得出答案;
(2)利用等边三角形的性质结合勾股定理得出答案.
解答  解:(1)如图所示:⊙O即为所求.
解:(1)如图所示:⊙O即为所求.
(2)连结OA,作OD⊥AB于点D,
则AD=$\frac{1}{2}$AB=3,∠OAD=30°,OA=$\frac{1}{2}$OD,
在Rt△OAD中,设OA=x,
则${x^2}={({\frac{x}{2}})^2}+{3^2}$,
解得:$x=2\sqrt{3}$,
故⊙O的半径为$2\sqrt{3}$.
点评 此题主要考查了复杂作图以及勾股定理等知识,正确确定圆心的位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.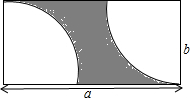 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )
 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )| A. | ab-$\frac{π{a}^{2}}{4}$ | B. | ab-$\frac{π{b}^{2}}{2}$ | C. | ab-$\frac{π{a}^{2}}{2}$ | D. | ab-$\frac{π{b}^{2}}{4}$ |
18.三角形两边的长分别是4和3,第三边的长是一元二次方程x2-6x+5=0的一个实数根,则该三角形的周长是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 8或12 |
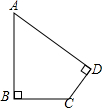 有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2.
有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).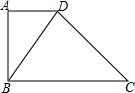 如图,已知四边形ABCD中,∠A=90°,AD∥BC.
如图,已知四边形ABCD中,∠A=90°,AD∥BC. 圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.
圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.