题目内容
 如图,在?ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接AG、BH、CE、DF相交于I、J、K、L,若?ABCD的面积为1,求四边形IJKL的面积.
如图,在?ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接AG、BH、CE、DF相交于I、J、K、L,若?ABCD的面积为1,求四边形IJKL的面积.考点:面积及等积变换
专题:
分析:延长BH、CD交于点N,易证△ABH≌△DNH,则有AB=DN,进而可得BE=
CN,易证△BIE∽△NIC,则有
=
=
.易证四边形AECG是平行四边形,则有AG∥EC,同理可得BH∥FD,从而有四边形IJKL是平行四边形.易证△CFJ∽△CBI,可得IJ=CJ=
CI,设EI=x,则IC=4x,IJ=2x,EC=5x,从而有
=
=
,
=
=
=
,由S?ABCD=1就可求出四边形IJKL的面积.
| 1 |
| 4 |
| EI |
| CI |
| BE |
| NC |
| 1 |
| 4 |
| 1 |
| 2 |
| S?AECG |
| S?ABCD |
| AE |
| AB |
| 1 |
| 2 |
| S?IJKL |
| S?AECG |
| IJ |
| EC |
| 2x |
| 5x |
| 2 |
| 5 |
解答: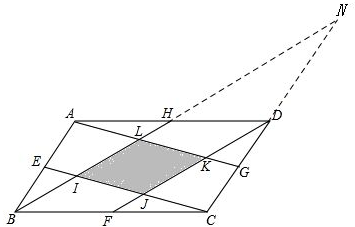 解:延长BH、CD交于点N,如图.
解:延长BH、CD交于点N,如图.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABH=∠DNH.
在△ABH和△DNH中,
,
∴△ABH≌△DNH(AAS),
∴AB=DN,
∴AB=
CN.
∵点E是AB的中点,
∴BE=
AB,
∴BE=
CN.
∵AB∥CN,
∴△BIE∽△NIC,
∴
=
=
.
∵G是CD的中点,
∴CG=
CD,
∴AE=CG.
∵AE∥CG,
∴四边形AECG是平行四边形.
∴AG∥EC.
同理可得:BH∥FD,
∴四边形IJKL是平行四边形.
∵BH∥FD,
∴△CFJ∽△CBI,
∴
=
=
,
∴IJ=CJ=
CI,
设EI=x,则IC=4x,IJ=2x,EC=5x.
∵
=
=
,
=
=
=
,
∵S?ABCD=1,∴S?AECG=
,
∴S?IJKL=
×
=
.
∴四边形IJKL的面积为
.
 解:延长BH、CD交于点N,如图.
解:延长BH、CD交于点N,如图.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABH=∠DNH.
在△ABH和△DNH中,
|
∴△ABH≌△DNH(AAS),
∴AB=DN,
∴AB=
| 1 |
| 2 |
∵点E是AB的中点,
∴BE=
| 1 |
| 2 |
∴BE=
| 1 |
| 4 |
∵AB∥CN,
∴△BIE∽△NIC,
∴
| EI |
| CI |
| BE |
| NC |
| 1 |
| 4 |
∵G是CD的中点,
∴CG=
| 1 |
| 2 |
∴AE=CG.
∵AE∥CG,
∴四边形AECG是平行四边形.
∴AG∥EC.
同理可得:BH∥FD,
∴四边形IJKL是平行四边形.
∵BH∥FD,
∴△CFJ∽△CBI,
∴
| CJ |
| CI |
| CF |
| CB |
| 1 |
| 2 |
∴IJ=CJ=
| 1 |
| 2 |
设EI=x,则IC=4x,IJ=2x,EC=5x.
∵
| S?AECG |
| S?ABCD |
| AE |
| AB |
| 1 |
| 2 |
| S?IJKL |
| S?AECG |
| IJ |
| EC |
| 2x |
| 5x |
| 2 |
| 5 |
∵S?ABCD=1,∴S?AECG=
| 1 |
| 2 |
∴S?IJKL=
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
∴四边形IJKL的面积为
| 1 |
| 5 |
点评:本题考查了面积及等级变换、平行四边形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质等知识,证明四边形IJKL是平行四边形并求出
是解决本题的关键.
| IJ |
| EC |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠ACB=90°,D为AB的中点,已知CD=1cm,则AB的长为
如图,∠ACB=90°,D为AB的中点,已知CD=1cm,则AB的长为 如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,求证:PQ=PB+DQ.
如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,求证:PQ=PB+DQ.