题目内容
（1）
•(
)2÷
；
（2）（x+3）2-（x+2）（x-1）；
（3）（12x2y-6xy3）÷（-3xy）；
（4）（x-y+9）（x+y-9）．
| 2m |
| 3n |
| 3n |
| p |
| mn |
| p2 |
（2）（x+3）2-（x+2）（x-1）；
（3）（12x2y-6xy3）÷（-3xy）；
（4）（x-y+9）（x+y-9）．
考点：分式的混合运算,整式的混合运算,因式分解的应用
专题：计算题
分析：（1）先进行幂的乘方运算和除法运算化为乘法运算得到原式=
•
•
，然后约分即可；
（2）先利用乘法公式展开，然后去括号后合并同类项即可；
（3）把多项式的每一项分别除以-3xy，然后根据同底数幂的除法法则运算即可；
（4）先变形得到原式=[x-（y-9）][x+（y-9）]，则可利用平方差公式计算，然后再利用完全平方公式计算即可．
| 2m |
| 3n |
| 9n2 |
| p2 |
| p2 |
| mn |
（2）先利用乘法公式展开，然后去括号后合并同类项即可；
（3）把多项式的每一项分别除以-3xy，然后根据同底数幂的除法法则运算即可；
（4）先变形得到原式=[x-（y-9）][x+（y-9）]，则可利用平方差公式计算，然后再利用完全平方公式计算即可．
解答：解：（1）原式=
•
•
=6；
（2）原式=x2+6x+9-（x2+x-2）
=x2+6x+9-x2-x+2
=5x+11；
（3）原式=12x2y÷（-3xy）-6xy3÷（-3xy）
=-4x+2y2；
（4）原式=[x-（y-9）][x+（y-9）]
=x2-（y-9）2
=x2-（y2-18y+81）
=x2-y2+18y-81．
| 2m |
| 3n |
| 9n2 |
| p2 |
| p2 |
| mn |
=6；
（2）原式=x2+6x+9-（x2+x-2）
=x2+6x+9-x2-x+2
=5x+11；
（3）原式=12x2y÷（-3xy）-6xy3÷（-3xy）
=-4x+2y2；
（4）原式=[x-（y-9）][x+（y-9）]
=x2-（y-9）2
=x2-（y2-18y+81）
=x2-y2+18y-81．
点评：本题考查了分式的混合运算：要注意运算顺序，式与数有相同的混合运算顺序；先乘方，再乘除，然后加减，有括号的先算括号里面的．也考查了整式的混合运算．
练习册系列答案
相关题目
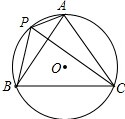如图，A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°．