题目内容
3.已知点P到⊙O最远点的距离是m,最近点的距离为n,则这个圆的半径是( )| A. | $\frac{m+n}{2}$ | B. | $\frac{m-n}{2}$ | C. | $\frac{m+n}{2}或\frac{m-n}{2}$ | D. | $\frac{1}{2}mn$ |
分析 已知的点可能在圆外,也可能在圆内,分两种情况进行讨论.
解答 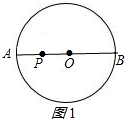 解:本题没有明确告知点的位置,应分点在圆内与圆外两种情况,
解:本题没有明确告知点的位置,应分点在圆内与圆外两种情况,
①当点P在⊙O内时,如图1所示:
此时PA=n,PB=m,
∴AB=m+n,
因此半径为$\frac{m+n}{2}$;
②当点P在⊙O外时,如图2所示: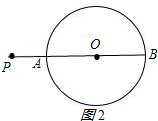 此时PA=n,PB=m,直线PB过圆心O,
此时PA=n,PB=m,直线PB过圆心O,
直径AB=PB-PA=m-n,
因此半径为$\frac{m-n}{2}$;
综上所述:这个圆的半径为$\frac{m+n}{2}$或$\frac{m-n}{2}$;
故选:C.
点评 本题考查了点与圆的位置关系;解决本题要注意点与圆的位置关系,这个点可能在圆外也可能在圆内,所以分两种情况讨论是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.从1-9这九个数字中任选三个数字,由这三个数字中的任意两个数字组成两位数,可以组成六个两位数,先把这六个两位数相加,然后用所得的和除以所选三个数字之和,结果是( )
| A. | 21 | B. | 20 | C. | 22 | D. | 不能确定 |
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3+2$\sqrt{2}$=5$\sqrt{2}$ | C. | 2$\sqrt{3}$×3$\sqrt{3}$=18 | D. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{2}$ |
