题目内容
14.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.

分析 (1)根据余角的性质得到∠DEC=∠BAC,由于∠DEC+∠BEC=180°,即可得到结论;
(2)根据角平分线的性质得到∠EBC=$\frac{1}{2}∠$ABC,∠ECB=$\frac{1}{2}∠$ACB,于是得到结论;
(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°+$\frac{1}{2}∠$BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
解答 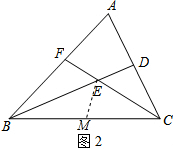 解:(1)∵BD⊥AC,CF⊥AB,
解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=$\frac{1}{2}∠$ABC,∠ECB=$\frac{1}{2}∠$ACB,∠BEC=180°-(∠EBC+∠ECB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠BAC)=90°$+\frac{1}{2}$∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+$\frac{1}{2}∠$BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
$\left\{\begin{array}{l}{∠FBE=∠EBM}\\{BE=BE}\\{∠FEB=∠MEB}\end{array}\right.$,
∴△FBE≌△EBM,
∴EF=EM,同理DE=EM,
∴EF=DE.
点评 本题考查了全等三角形的判定和性质,角平分线的定义,垂直的定义,正确的作出辅助线构造全等三角形是解题的关键.

| A. | 3.8×109 | B. | 3.8×1010 | C. | 3.8×1011 | D. | 3.8×108 |
| A. | 4.3×106米 | B. | 4.3×10-5米 | C. | 4.3×10-6米 | D. | 43×107米 |
| A. | $\frac{m+n}{2}$ | B. | $\frac{m-n}{2}$ | C. | $\frac{m+n}{2}或\frac{m-n}{2}$ | D. | $\frac{1}{2}mn$ |