题目内容
13.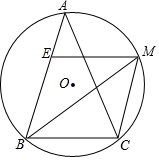 如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
分析 根据角平分线的定义得到∠EBM=∠CBM=$\frac{1}{2}∠$ABC,等量代换得到∠ABM=∠BMC=∠CBM,根据平行线的判定和等腰三角形的判定得到BE∥CM,BC=CM,然后根据菱形的判定定理即可得到结论.
解答 解:四边形EBCM是菱形,
理由:∵BM平分∠ABC交外接圆于点M,
∴∠EBM=∠CBM=$\frac{1}{2}∠$ABC,
∵∠ABC=2∠A,
∴∠A=∠ABM=∠CBM,
∵∠A=∠BMC,
∴∠ABM=∠BMC=∠CBM,
∴BE∥CM,BC=CM,
∵ME∥BC,
∴四边形EBCM是菱形.
点评 本题考查了角平分线的定义,平行线的判定,等腰三角形的性质,菱形的判定,熟练掌握各定理是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.-1+2-3+4-5+6+…-2015+2016的值等于( )
| A. | 1 | B. | -1 | C. | 2016 | D. | 1008 |
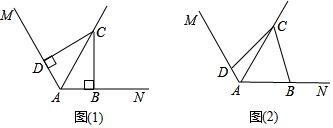
 平面直角坐标系中,△ABC的位置如图所示,已知OA=2OB,BC=5,△ABC的面积为5.
平面直角坐标系中,△ABC的位置如图所示,已知OA=2OB,BC=5,△ABC的面积为5.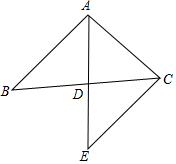 已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.
已知:如图,AD是△ABC中BC边上的中线,延长AD到E,使DE=AD.