题目内容
14.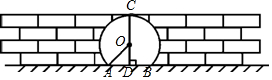 如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
分析 连接OA,由垂径定理易得出AD的长度,在Rt△OAD中,可用半径表示出OD的长,根据勾股定理即可求出半径的长度.
解答 解:连接OA;
Rt△OAD中,AD=$\frac{1}{2}$AB=1米;
设⊙O的半径为R,则OA=OC=R,OD=5-R;
由勾股定理,得:OA2=AD2+OD2,即:
R2=(5-R)2+12,解得R=2.6(米);
答:圆柱形门所在圆的半径是2.6米.
点评 此题主要考查的是垂径定理及勾股定理的应用.解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+( $\frac{a}{2}$)2成立,知道这三个量中的任意两个,就可以求出另外一个.

练习册系列答案
相关题目
4.已知a,b,c是正数,3a=4b=5c.若a+b=kc,则k=( )
| A. | $\frac{12}{35}$ | B. | $\frac{5}{7}$ | C. | $\frac{7}{5}$ | D. | $\frac{35}{12}$ |
5.说法正确的是( )
| A. | 有最小的负整数,有最大的正整数 | B. | 有最小的负数,没有最大的正数 | ||
| C. | 有最大的负数,没有最大的正数 | D. | 没有最大的有理数和最小的有理数 |
19.若ab≠1,且有5a2+2001a+9=0及9b2+2001b+5=0,则$\frac{a}{b}$的值是( )
| A. | $\frac{9}{5}$ | B. | $\frac{5}{9}$ | C. | $-\frac{2001}{5}$ | D. | $-\frac{2001}{9}$ |
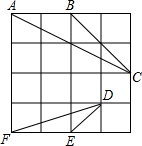 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.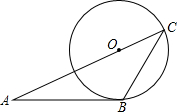 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧$\widehat{BC}$的度数为120°.
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧$\widehat{BC}$的度数为120°.