题目内容
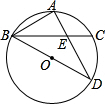
3.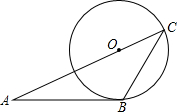 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧$\widehat{BC}$的度数为120°.
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧$\widehat{BC}$的度数为120°.
分析 连接OB,如图,根据切线的性质得∠ABO=90°,则∠OBC=30°,根据等腰三角形的性质和三角形内角和可得到∠BOC=120°,然后根据弧的度数等于它所对的圆心角的度数.
解答  解:连接OB,如图,
解:连接OB,如图,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∵∠ABC=120°,
∴∠OBC=30°,
而OB=OC,
∴∠C=∠OBC=30°,
∴∠BOC=120°,
∴弧$\widehat{BC}$的度数为120°.
故答案为120°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆心角、弧、弦的关系.

练习册系列答案
相关题目

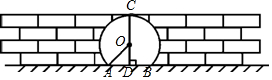 如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?
如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?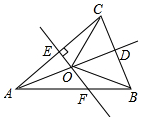 如图,已知△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,求证:点O在AB的垂直平分线上.
如图,已知△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,求证:点O在AB的垂直平分线上.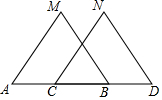 如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN.
如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN. 如图,△ABC的三个顶点都在⊙O上,AD为⊙O的直径,AE⊥BC于点E,交⊙O于点F.求证:∠1=∠2.
如图,△ABC的三个顶点都在⊙O上,AD为⊙O的直径,AE⊥BC于点E,交⊙O于点F.求证:∠1=∠2.
 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4