题目内容
13.抛物线y=x2+bx+c过点(1,0),与x轴两交点间距离为3,则b、c的值为b=-5,c=4或b=-1,c=-2.分析 利用抛物线与x轴的一个交点为(1,0),抛物线与x轴两交点间距离为3,易得抛物线与x轴的另一个交点为(4,0)或(-2,0),则利用交点式可得到抛物线解析式,然后把解析式化为一般式即可得到b、c的值.
解答 解:因为抛物线y=x2+bx+c与x轴的一个交点为(1,0),
而抛物线与x轴两交点间距离为3,
所以抛物线与x轴的另一个交点为(4,0)或(-2,0),
当抛物线y=x2+bx+c与x轴的交点为(1,0)和(4,0)时,抛物线解析式为y=(x-1)(x-4)=x2-5x+4,则b=-5,c=4;
当抛物线y=x2+bx+c与x轴的交点为(1,0)和(-2,0)时,抛物线解析式为y=(x-1)(x+2)=x2-x-2,则b=-1,c=-2;
故答案为b=-5,c=4或b=-1,c=-2.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
16. 将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
 将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )| A. | 140° | B. | 160° | C. | 170° | D. | 150° |
5.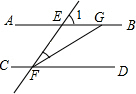 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )| A. | 122° | B. | 151° | C. | 116° | D. | 97° |
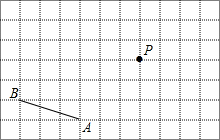 如图,在7×11网格中,已知线段AB和点P,按下列要求画图.
如图,在7×11网格中,已知线段AB和点P,按下列要求画图.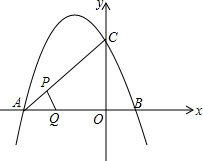 如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.
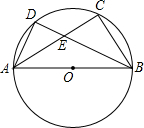 如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DC}$,AB=10,BD=8,则AE=$\frac{15}{2}$.
如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DC}$,AB=10,BD=8,则AE=$\frac{15}{2}$.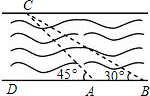 如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)