题目内容
2.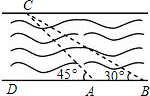 如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 设河宽为未知数,那么可利用三角函数用河宽表示出AE、EB,然后根据BE-AE=50就能求得河宽.
解答 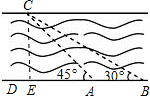 解:过C作CE⊥AB于E,设CE=x米,
解:过C作CE⊥AB于E,设CE=x米,
在Rt△AEC中:∠CAE=45°,AE=CE=x
在Rt△BCE中:∠CBE=30°,BE=$\sqrt{3}$CE=$\sqrt{3}$x,
∴$\sqrt{3}$x=x+50解之得:x=25$\sqrt{3}$+25≈68.31.
答:河宽为68.31米.
点评 此题主要考查了三角函数的概念和应用,解题关键是把实际问题转化为数学问题,抽象到三角形中,利用三角函数进行解答.

练习册系列答案
相关题目
10.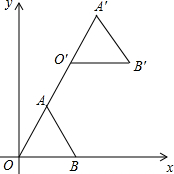 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
 如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )| A. | (4,2$\sqrt{3}$) | B. | (3,3$\sqrt{3}$) | C. | (4,3$\sqrt{3}$) | D. | (3,2$\sqrt{3}$) |
11.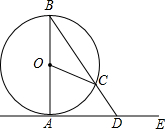 如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
 如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 20° |
12.下列四个图形中,线段BE是△ABC的高的是( )
| A. | 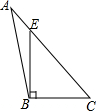 | B. | 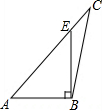 | C. | 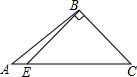 | D. | 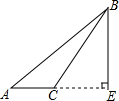 |
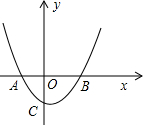 如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.