题目内容
18．
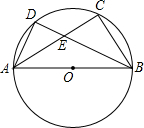如图，AB是⊙O的直径，$\widehat{AD}$=$\widehat{DC}$，AB=10，BD=8，则AE=$\frac{15}{2}$．
分析 根据AB是⊙O的直径，$\widehat{AD}$=$\widehat{DC}$，推出△ABD∽△ADE，列出比例式即可得到结论．
解答 解：∵AB是⊙O的直径，
∴∠D=90°，
∵AB=10，BD=8，
∴AD=$\sqrt{{AB}^{2}{+BD}^{2}}$=6，
∵$\widehat{AD}$=$\widehat{DC}$，
∴∠ABD=∠CAD，
∴△ABD∽△ADE，
∴$\frac{AB}{AE}=\frac{BD}{AD}$，
∴$\frac{10}{AE}=\frac{8}{6}$，
∴AE=$\frac{15}{2}$，
故答案为：$\frac{15}{2}$．
点评 本题考查了相似三角形的判定和性质，勾股定理，圆周角定理，证得△ABD∽△ADE是解题的关键．
练习册系列答案
相关题目
10．
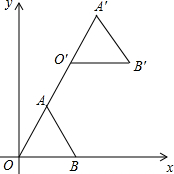如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）
如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）| A． | （4，2$\sqrt{3}$） | B． | （3，3$\sqrt{3}$） | C． | （4，3$\sqrt{3}$） | D． | （3，2$\sqrt{3}$） |
8．一个不透明的布袋中，放有3个白球，5个红球，它们除颜色外完全相同，从中随机摸取1个，摸到红球的概率是（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{3}$ |