题目内容
6.解不等式:(1)求不等式1-2x<6的所有负整数解.
(2)$\frac{1}{3}$(1-2x)$≥\frac{3(2x-1)}{2}$(在数轴上把解集表示出来)
分析 (1)先移项,合并同类项,把x的系数化为1即可;
(2)先去分母,再去括号,移项,合并同类项,把x的系数化为1即可.
解答 解:(1)移项得,-2x<6-1,
合并同类项得,-2x<5,
把x的系数化为1得,x>-$\frac{5}{2}$;
(2)去分母得,2(1-2x)≥9(2x-1)
去括号得,2-4x≥18x-9,
移项得,-4x-18x≥-9-2,
合并同类项得,-22x≥-11,
把x的系数化为1得,x≤$\frac{1}{2}$.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
16.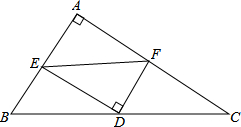 如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
 如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )| A. | 7 | B. | 6 | C. | 5 | D. | $\sqrt{13}$ |
17.一元二次方程x2+x+$\frac{1}{4}$=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
15. 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )
 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )| A. | a的相反数大于2 | B. | a的相反数是2 | C. | |a|>2 | D. | 2a<0 |