题目内容
5.为了节省空间,时尚装修的设计师设计出一款餐桌,餐桌的两边翻开后会成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2),小华用皮带尺量出AC=1.6米,AB=0.8米,那么桌面翻成圆桌后,桌子面积会增加$\frac{32π}{75}-\frac{8\sqrt{3}}{25}$平方米.(结果保留π)
分析 如图,首先求出∠BOC的度数,然后分别求出扇形OBC、△OBC的面积,进而求出弓形BnC的面积,即可解决问题.
解答 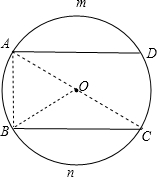 解:如图,连接OB;由题意得:∠ABC=90°,
解:如图,连接OB;由题意得:∠ABC=90°,
∵sin∠C=$\frac{AB}{AC}=\frac{0.8}{1.6}=\frac{1}{2}$,
∴∠C=30°;
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴∠BOC=120°,
∴S弓形BnC=S扇形OBC-S△OBC
=$\frac{120π•(0.8)^{2}}{360}-\frac{1}{2}×(0.8)^{2}•sin120°$
=$\frac{16π}{75}-\frac{4\sqrt{3}}{25}$,
∴桌面翻成圆桌后,桌子面积会增加2S弓形BnC=$\frac{32π}{75}-\frac{8\sqrt{3}}{25}$(平方米),
故答案为$\frac{32π}{75}-\frac{8\sqrt{3}}{25}$.
点评 该题主要考查了勾股定理、扇形面积的计算等知识点及其应用问题;解题的方法是将实际问题转化为数学中的几何问题;解题的关键是灵活运用勾股定理、扇形面积公式等来分析、解答.

练习册系列答案
相关题目
15.$\frac{1}{12}$是( )
| A. | 整数 | B. | 有限小数 | C. | 无限循环小数 | D. | 无限不循环小数 |
13.已知抛一枚均匀硬币正面朝上的概率为$\frac{1}{2}$,下列说法正确的是( )
| A. | 连续抛一枚均匀硬币2次必有1次正面朝上 | |
| B. | 连续抛一枚均匀硬币10次,不可能正面都朝上 | |
| C. | 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次 | |
| D. | 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的 |
 已知,∠DBC和∠BCE分别为△ABC的两个外角,探究∠A和∠DBC,∠BCE之间的数量关系.
已知,∠DBC和∠BCE分别为△ABC的两个外角,探究∠A和∠DBC,∠BCE之间的数量关系.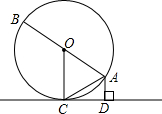 已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.