题目内容
1.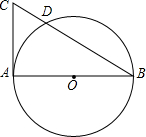 如图,AB为⊙O的直径,CA切⊙O于A,CB交⊙O于D,若CD=2,BD=6,求半径r=( )
如图,AB为⊙O的直径,CA切⊙O于A,CB交⊙O于D,若CD=2,BD=6,求半径r=( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 根据切割线定理CA2=CD•CB可得CA=4,然后在Rt△ABC中,利用CA=4,BC=8和勾股定理即可求出直径AB的长,进而可求出半径r的长度.
解答 解:∵CA切⊙O于A,
∴CA2=CD•CB,
又∵CD=2,BD=6,
∴CA=4.
在Rt△ABC中,CA=4,BC=8,
∴AB=$\sqrt{B{C}^{2}-C{A}^{2}}$=4$\sqrt{3}$,
∴半径r=$\frac{1}{2}$AB=2$\sqrt{3}$
故选A.
点评 本题考查了圆的切线性质,及勾股定理等知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
11.一元二次方程x2+2x=0的根是( )
| A. | x=0或x=-2 | B. | x=0或x=2 | C. | x=0 | D. | x=-2 |
12.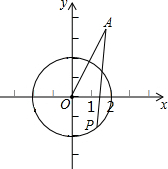 如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
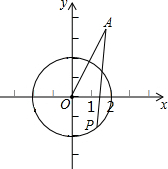 如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
9. 如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
 如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )
如图,若弧AB半径PA为15,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是( )| A. | 5周 | B. | 6周 | C. | 7周 | D. | 8周 |
6.学校组织春游,安排九年级三辆车,小明和小慧都可以从这三辆车中任选一辆搭乘,小明和小慧同车的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
13.已知抛一枚均匀硬币正面朝上的概率为$\frac{1}{2}$,下列说法正确的是( )
| A. | 连续抛一枚均匀硬币2次必有1次正面朝上 | |
| B. | 连续抛一枚均匀硬币10次,不可能正面都朝上 | |
| C. | 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次 | |
| D. | 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的 |