题目内容
5.先化简,再求值:$({\frac{{{x^2}-2x+1}}{{{x^2}-1}}+\frac{1}{x}})÷\frac{1}{x+1}$,其中x=2.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=[$\frac{(x-1)^{2}}{(x+1)(x-1)}$+$\frac{1}{x}$]•(x+1)
=[$\frac{x-1}{x+1}$+$\frac{1}{x}$]•(x+1)
=$\frac{{x}^{2}+1}{x(x+1)}$•(x+1)
=$\frac{{x}^{2}+1}{x}$,
当x=2时,原式=$\frac{{2}^{2}+1}{2}$=$\frac{5}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.若分式$\frac{3}{x-2}$有意义,则x应满足的条件是( )
| A. | x≠0 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
17.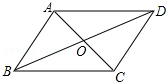 如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
 如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )| A. | AB=DC,AD=BC | B. | AB∥DC,AO=BO | C. | AB=DC,∠B=∠D | D. | AB∥DC,∠B=∠D |
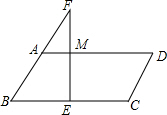 如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F.若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为( )
如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F.若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为( )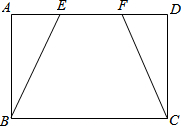 如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间为t(s)
如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间为t(s)