题目内容
17. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 60° | B. | 55° | C. | 50° | D. | 无法计算 |
分析 求出∠BAD=∠CAE,根据SAS推出△BAD≌△CAE,根据全等三角形的性质求出∠ABD=∠2=30°,根据三角形的外角性质求出即可.
解答 解:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△BAD≌△CAE,
∵∠2=30°,
∴∠ABD=∠2=30°,
∵,∠1=25°,
∴∠3=∠ABD+∠1=55°,
故选B.
点评 本题考查了全等三角形的性质和判定,三角形的外角性质的应用,能求出△BAD≌△CAE是解此题的关键,注意:全等三角形的对应角相等.

练习册系列答案
相关题目
7.下列数据中,能构成三角形的是( )
| A. | 1,2,4 | B. | 4,5,9 | C. | 20,15,8 | D. | 5,15,8 |
8.下列去括号正确的是( )
| A. | -(3x+7)=-3x+7 | B. | -$\frac{1}{3}$(6x-3)=-2x+3 | C. | $\frac{1}{5}$(3m-5n)=$\frac{3}{5}$m+n | D. | -($\frac{2}{3}$m-2a)=-$\frac{2}{3}$m+2a |
 如图是一次函数y=kx+2的图象,则方程kx=-2的解为x=-1.
如图是一次函数y=kx+2的图象,则方程kx=-2的解为x=-1.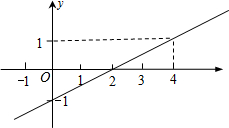 已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个.
已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个. 如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.
如图,O是△ABC内一点,BO=CO,∠ABO=∠ACO,求证:AO平分∠BAC.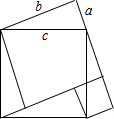 (1)画出“弦图”,并利用“弦图”证明勾股定理.
(1)画出“弦图”,并利用“弦图”证明勾股定理.