题目内容

5．$\sqrt{10}$是无理数，设它的整数部分为a，小数部分为b，则a-b的值为（　　）
A．2和3之间B．3和4之间C．4和5之间D．5和6之间

分析 由于3＜$\sqrt{10}$＜4，所以可求出a，进而求出b，则a-b的范围即可求得．

解答 解：∵$\sqrt{9}$＜$\sqrt{10}$＜$\sqrt{16}$，
∴3＜$\sqrt{10}$＜4，
∴$\sqrt{10}$的整数部分a=3，
∴小数部分b=$\sqrt{10}$-3，
∴a-b=3-（$\sqrt{10}$-3）=6-$\sqrt{10}$，
又∵-4＜-$\sqrt{10}$＜-3，
∴2＜6-$\sqrt{10}$＜3．
故选：A．

点评 此题主要考查了无理数的估算，解决问题的关键是根据3＜$\sqrt{10}$＜4进行判断．

练习册系列答案
相关题目
15．如图，抛物线y=-x2+bx+c与x轴交于A（-1，0），B两点（点A在点B的左侧），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．
（1）求抛物线的解析式；
（2）当点P在线段OB上运动时，求线段MN的最大值；
（3）是否存在点P，使得以点C、O、M、N为顶点的四边形是平行四边形？若存在，请直接写出m的值；若不存在，请说明理由．
16．深圳市统计局发布的2016年《深圳市气候数据每日观测记录》显示，2016年12月26日=--31日这六天的平均相对湿度（百分数）分别是58，50，45，54，64，82，对于这组数据，以下说法正确的是（　　）
A．平均数是59B．中位数是56C．众数是82D．方差是37
13．如图所示的几何体的俯视图是（　　）
A．B．C．D．
20．如图，直线a∥b．下列关系判断正确的是（　　）
A．∠1+∠2=180°B．∠1+∠2=90°C．∠1=∠2D．无法判断
10．不等式组$\left\{\begin{array}{l}{x-1＞0}\\{4x≤8}\end{array}\right.$的解集在数轴上表示为（　　）
A．B．C．D．
17．下列等式从左到右的变形属于因式分解的是（　　）
A．x2-2x+1=（x-1）2B．ax-ay+a=a（x-y）+a
C．x3-x=x（x+1）（x-1）+1D．x2-4+3x=（x+2）（x-2）+3x
14．太阳的表面温度大约有6000℃，而太阳中心的温度达到了1920万℃，其中“1920万”用科学记数法可将表示为（　　）
A．1.92×103B．1.92×107C．19.2×102D．0.192×108
15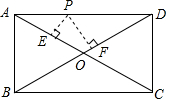．如图，P是矩形ABCD的边AD上一个动点，PE⊥AC于E，PF⊥BD于F，当P从A向D运动（P与A，D不重合），则PE+PF的值（　　）
A．增大B．减小C．不变D．先增大再减小

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网