题目内容
10.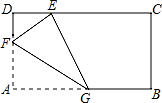 已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长.
已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长.
分析 由翻折的性质可知:AF=EF=$\frac{2}{3}$,∠EFG=∠AFG,从而可知cos∠EFD=$\frac{1}{2}$,故此可求得∠DFE=60°,∠AFG=60°,然后再△AFG中利用特殊锐角三角函数值可求得FG,AG的长,从而可求得GB的长,最后计算出周长即可.
解答 解:∵AD=1,AF=$\frac{2}{3}$,
∴DF=$\frac{1}{3}$.
由翻折的性质可知:AF=EF=$\frac{2}{3}$,∠EFG=∠AFG.
在Rt△DEF中,cos∠EFD=$\frac{DF}{EF}=\frac{\frac{1}{3}}{\frac{2}{3}}$=$\frac{1}{2}$.
∴∠DFE=60°.
∴∠AFG=$\frac{1}{2}×(180°-60°)$=60°.
在Rt△AFG中,$\frac{FG}{AF}=\frac{1}{2}$,$\frac{AG}{AF}=\sqrt{3}$,∴FG=2AF=$\frac{4}{3}$,AG=$\sqrt{3}$AF=$\frac{2\sqrt{3}}{3}$.
∴GB=2-$\frac{2\sqrt{3}}{3}$=$\frac{6-2\sqrt{3}}{3}$.
∴五边形的DFGBC的周长=DF+FG+GB+BC+CD=$\frac{1}{3}$+$\frac{4}{3}$+$\frac{6-2\sqrt{3}}{3}$+1+2=$\frac{20-\sqrt{3}}{3}$.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值,由特殊度数的锐角三角函数值求得∠DFE=60°是解题的关键.

练习册系列答案
相关题目
20. 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
(1)本次调查的样本容量为200;在频数分布表中,a的值为60,b的值为0.05,并将频数分布直方图补充完整;
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
15.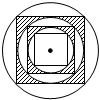 如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
 如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )
如图,在半径为1的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此类推,第6个内切圆的面积是( )| A. | $\frac{π}{16}$ | B. | $\frac{π}{32}$ | C. | $\frac{π}{64}$ | D. | $\frac{π}{128}$ |
2.如果两个相似三角形对应高的比为3:5,面积之比为2:x,那么x的算术平方根为( )
| A. | $\frac{5\sqrt{2}}{3}$ | B. | $±\frac{5\sqrt{2}}{3}$ | C. | $\frac{50}{9}$ | D. | $±\frac{50}{9}$ |
19.对角线互相平分的四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
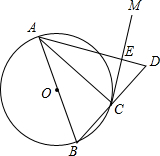 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.