题目内容
19.已知一个凸四边形ABCD的边长顺次为a,b,c,d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,试判断这个四边形是否是中心对称图形.分析 由a2+ab-ac-bc=0分解因式,可得到(a+b)(a-c)=0,得a=c,再由b2+bc-bd-cd=0,可得到b=d,则四边形的两组对边分别相等,所以四边形ABCD一定是平行四边形,再根据中心对称图形的定义即可判断.
解答 解:由a2+ab-ac-bc=0,可知(a+b)(a-c)=0,则a-c=0,即a=c;
由b2+bc-bd-cd=0,可知(b+c)(b-d)=0;则b-d=0,即b=d.
(其中a,b,c,d都是正数,a+b、b+c一定不等于0)
由a=c;b=d知四边形ABCD的两组对边分别相等,则四边形ABCD一定是平行四边形,
所以这个四边形是中心对称图形.
点评 本题考查了因式分解的应用,平行四边形的判定,中心对称图形的定义,解决本题的关键是应用因式分解的知识得到四边形对边的关系.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
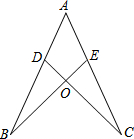 如图,已知:AB=AC,AE=AD,求证:OB=OC.
如图,已知:AB=AC,AE=AD,求证:OB=OC.