题目内容
9.在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②-①得2S-S=27-1,S=27-1,即1+2+22+23+24+25+26=27-1.(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2016(a≠0且a≠1)的值.
分析 (1)依照题意设设S=1+3+32+33+34+35+36值,然后在其两边同乘以3得3S=.3+32+33+34+35+36..+37,再求出两式的差变形即可.
(2)可仿照(1)求解.
解答 解:(1)设S=1+3+32+33+34+35+36…①
则:3S=.3+32+33+34+35+36..+37…②
②-①得:2S=37-1
即:1+3+32+33+34+35+36=$\frac{1}{2}$(37-1).
(2)设S=1+a+a2+a3+…+a2016…①
∵a≠0
∴aS=a+a2+a3+…+a2016+a2017…②
②-①得:(a-1)S=a2017-1
∵a≠1
∴S=$\frac{{a}^{2017}-1}{a-1}$
即:1+a+a2+a3+…+a2016=$\frac{{a}^{2017}-1}{a-1}$
点评 本题考查了数字的变化规律、有理数的混合运算等知识点,解题的关键是理解题目中所体现的一种解题方法与思路,培养学生的自学能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
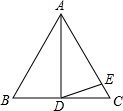 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°.
如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°. 要设计一幅长30cm,宽20cm的图案,制成一幅矩形挂图,如图所示,其中有两横两竖的彩条(横竖彩条的宽度相等).如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度?设彩条的宽为x cm,那么x满足的方程为(30-2x)(20-2x)=30×20×(1-$\frac{1}{4}$).
要设计一幅长30cm,宽20cm的图案,制成一幅矩形挂图,如图所示,其中有两横两竖的彩条(横竖彩条的宽度相等).如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度?设彩条的宽为x cm,那么x满足的方程为(30-2x)(20-2x)=30×20×(1-$\frac{1}{4}$).