题目内容
8. 如图,在△ABC中,AD平分∠BAC,AB=AD,∠1=∠2,使BE交于AD延长线于E,连接EC,过A作AF⊥EC于F交BC于G,下列结论:①∠AEB=∠ACB,②BE=CD,③S△AGC=$\frac{AG•EF}{2}$,④∠2=2∠3,其中正确有( )个.
如图,在△ABC中,AD平分∠BAC,AB=AD,∠1=∠2,使BE交于AD延长线于E,连接EC,过A作AF⊥EC于F交BC于G,下列结论:①∠AEB=∠ACB,②BE=CD,③S△AGC=$\frac{AG•EF}{2}$,④∠2=2∠3,其中正确有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①由∠1=∠2,利用角平分线的性质可得∠2=∠CAE,可得A,B,C,E四点共圆,由圆周角定理可得结论;②证明△ABE≌△ADC,利用全等三角形的性质可得结论;③由△ABE≌△ADC,易得AC=AE,由等腰三角形的性质易得CF=EF,得△AGC的面积;④由△AEC为等腰三角形易得∠EAF=∠CAF,可得结论.
解答 解:①∵AD平分∠BAC,
∴∠1=∠EAC,
∵∠1=∠2,
∴∠2=∠EAC,
∴A,B,C,E四点共圆,
∴∠AEB=∠ACB,
故此选项正确;
②在△ABE与△ADC中,
$\left\{\begin{array}{l}{∠ACB=∠AEB}\\{∠CAD=∠DAB}\\{AD=AB}\end{array}\right.$,
∴△ABE≌△ADC(AAS),
∴BE=DC,
故此选项正确;
③∵△ABE≌△ADC,
∴AE=AC,
∵AF⊥EC,
∴EF=CF,
∵S△AGE=$\frac{1}{2}•$AG•CF=$\frac{AG•EF}{2}$,
故此选项正确;
④∵△EAC为等腰三角形,
∴∠EAF=∠3=$\frac{1}{2}$∠EAC=$\frac{1}{2}$∠2,
∴∠2=2∠3,
故此选项正确;
∴正确的有4个选项,
故选D.
点评 本题主要考查了角平分线的性质,等腰三角形的性质等,综合运用各性质定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知a,b,c是两两不相等的实数,则方程(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0根的情况为( )
| A. | 必有两个不相等的实根 | B. | 没有实根 | ||
| C. | 必有两个相等的实根 | D. | 方程的根有可能取值a,b,c |
16.平行四边形一边长10cm,那么它的两条对角线的长可能是( )
| A. | 10cm和8cm | B. | 13cm和7cm | C. | 9cm和9cm | D. | 9cm和12cm |
20.在实数$\root{3}{-27}$,0.101 001 0001,π,$\sqrt{5}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
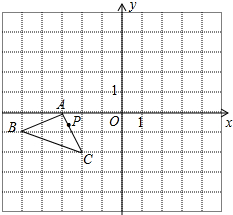 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)