题目内容
7．已知a，b，c是两两不相等的实数，则方程（x-a）（x-b）+（x-b）（x-c）+（x-c）（x-a）=0根的情况为（ ）| A． | 必有两个不相等的实根 | B． | 没有实根 | ||
| C． | 必有两个相等的实根 | D． | 方程的根有可能取值a，b，c |
分析 把原方程整理得3x2-（2a+2b+2c）x+（ab+bc+ac）=0，进一步利用根的判别式分析判断即可．
解答 解：∵（x-a）（x-b）+（x-b）（x-c）+（x-c）（x-a）=0，
∴3x2-（2a+2b+2c）x+（ab+bc+ac）=0，
则△=（2a+2b+2c）2-12（ab+bc+ac）
=4（a2+b2+c2-ab-ac-bc）
=2[（a-b）2+（b-c）2+（a-c）2]
∵a，b，c是两两不相等的实数，
∴2[（a-b）2+（b-c）2+（a-c）2]＞0，
∴方程必有两个不相等的实根．
故选：A．
点评 此题考查根的判别式，掌握根的情况与系数关系是解决问题的关键．
练习册系列答案
相关题目
如图，已知Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°，连接BC与DE相交于点F，连接CD、BE，求证：CF=EF．
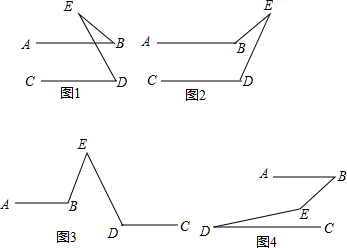
如图，以五边形的每个顶点为圆心，以1为半径画圆，求圆与五边形重合的阴影部分的面积．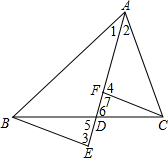
如图，AD是△ABC的角平分线，BE⊥AD于E，CF⊥AD于F，求证：$\frac{AB}{AC}$=$\frac{DE}{DF}$．
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的值．
如图，在△ABC中，AD平分∠BAC，AB=AD，∠1=∠2，使BE交于AD延长线于E，连接EC，过A作AF⊥EC于F交BC于G，下列结论：①∠AEB=∠ACB，②BE=CD，③S△AGC=$\frac{AG•EF}{2}$，④∠2=2∠3，其中正确有（ ）个．