题目内容
7. 如图,在平面直角坐标系中,△AOB是等腰三角形,其中OA=OB=2,∠AOB=30°.
如图,在平面直角坐标系中,△AOB是等腰三角形,其中OA=OB=2,∠AOB=30°.(1)若反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点B,求反比例函数的表达式;
(2)将△AOB绕点O顺时针方向旋转,旋转角为α(0°<α<360°).在旋转的过程中,点A,B能否同时落在(1)中反比例函数的图象上?若能,请求出α的值;若不能,则说明理由.
分析 (1)首先过点B作BC⊥x轴于点C,由OA=OB=2,∠AOB=30°,可求得OC与BC的长,即可求得点B的坐标,继而求得答案;
(2)首先过点B′作B′C⊥x轴于点C,当点A′与点B重合时,A′(1,$\sqrt{3}$),∠AOB′=2∠AOB=60°,继而求得点B′的坐标,则可得点A′与B′都在反比例函数上,继而求得答案.
解答 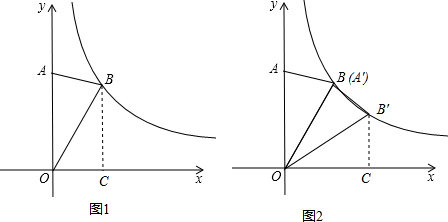 解:(1)如图1,过点B作BC⊥x轴于点C,
解:(1)如图1,过点B作BC⊥x轴于点C,
∵OA=OB=2,∠AOB=30°,
∴∠BOC=60°,
∴∠OBC=30°,
∴OC=$\frac{1}{2}$OB=1,
∴BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∴点B(1,$\sqrt{3}$),
∴k=1×$\sqrt{3}$=$\sqrt{3}$,
∴反比例函数的表达式为:y=$\frac{\sqrt{3}}{x}$;
(2)如图2,过点B′作B′C⊥x轴于点C,
当点A′与点B重合时,A′(1,$\sqrt{3}$),∠AOB′=2∠AOB=60°,
∴∠B′OC=30°,
∴B′C=$\frac{1}{2}$OB′=1,
∴OC=$\sqrt{OB{′}^{2}-B′{C}^{2}}$=$\sqrt{3}$,
∴点B′($\sqrt{3}$,1)在反比例函数的图象上;
∴α=30°,
同理:当点A′,B′在第三象限时,α=210°;
综上可得:当α=30°或210°时,点A,B能否同时落在(1)中反比例函数的图象上.
点评 此题属于反比例函数的综合题,考查了待定系数法求反比例函数的解析式、旋转的性质以及含30°角的直角三角形的性质.注意准确作出辅助线是关键.

练习册系列答案
相关题目
19.如图放置的四个几何体中,主视图是圆形的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在同一平面直角坐标系中,画出函数y=-5x+1与y=0.5x-10的图象.
在同一平面直角坐标系中,画出函数y=-5x+1与y=0.5x-10的图象.
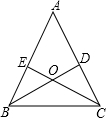 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.