题目内容
 如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.(1)求证:DF=EF;
(2)若△ABC的边长为a,BE的长为b,且a,b满足(a-5)2+b2-6b+9=0,求BF的长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)由DG∥AB,△ABC是等边三角形,可得出△CDG是等边三角形,由BE=CD,可得BE=DG,再求出△DFG≌△EFB,由全等三角形的性质即可得出结论;
(2)由(a-5)2+b2-6b+9=0,转化为:(a-5)2+(b-3)2=0,然后根据非负数的性质可得:a=5,b=3,即BC=5,CG=3,所以BG=2,由(1)知△DFG≌△EFB,所以FG=FB=
BG=1.
(2)由(a-5)2+b2-6b+9=0,转化为:(a-5)2+(b-3)2=0,然后根据非负数的性质可得:a=5,b=3,即BC=5,CG=3,所以BG=2,由(1)知△DFG≌△EFB,所以FG=FB=
| 1 |
| 2 |
解答:解:(1)∵△ABC是等边三角形,
∴∠C=∠A=∠ABC=60°,
∵DG∥AB,
∴∠CDG=∠A=60°,
∴△CDG是等边三角形,
∴CD=DG,
∵BE=CD,
∴BE=DG,
∵DG∥AB,
∴∠E=∠GDF,∠EBF=∠DGF,
在△DFG与△EFB中,
,
∴△DFG≌△EFB(ASA),
∴DF=FE;
(2)∵(a-5)2+b2-6b+9=0,
∴(a-5)2+(b-3)2=0,
∵(a-5)2≥0,(b-3)2≥0,
∴a-5=0,b-3=0,
∴a=5,b=3,
即BC=5,CG=3,
∴BG=2,
∵△DFG≌△EFB,
∴FG=FB=
BG=1.
∴∠C=∠A=∠ABC=60°,
∵DG∥AB,
∴∠CDG=∠A=60°,
∴△CDG是等边三角形,
∴CD=DG,
∵BE=CD,
∴BE=DG,
∵DG∥AB,
∴∠E=∠GDF,∠EBF=∠DGF,
在△DFG与△EFB中,
|
∴△DFG≌△EFB(ASA),
∴DF=FE;
(2)∵(a-5)2+b2-6b+9=0,
∴(a-5)2+(b-3)2=0,
∵(a-5)2≥0,(b-3)2≥0,
∴a-5=0,b-3=0,
∴a=5,b=3,
即BC=5,CG=3,
∴BG=2,
∵△DFG≌△EFB,
∴FG=FB=
| 1 |
| 2 |
点评:本题考查的是等边三角形的性质,根据题意得到△CDG是等边三角形是解答此题的关键.

练习册系列答案
相关题目
若一次函数y=mx+(m2+m-4)的图象与y轴的交点的纵坐标是8,则m的值为( )
| A、3和4 | B、-3和-4 |
| C、3和-4 | D、-3和4 |
 如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为
如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为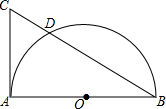 如图,AB是⊙O的直径,CA切⊙O于点A,CD=1cm,DB=3cm,求AB的长.
如图,AB是⊙O的直径,CA切⊙O于点A,CD=1cm,DB=3cm,求AB的长.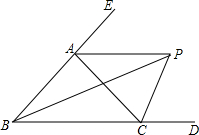 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P.