题目内容
9.(1)计算:$\sqrt{\frac{9}{4}}$-2sin30°+($\frac{1}{3}$)-1;(2)解不等式组:$\left\{\begin{array}{l}2x-1>3\\ \frac{x+1}{2}<\frac{2-x}{3}+2\end{array}\right.$.
分析 (1)原式利用算术平方根的定义,特殊角的三角函数值,以及负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=$\frac{3}{2}$-2×$\frac{1}{2}$+3=$\frac{7}{2}$;
(2)$\left\{\begin{array}{l}{2x-1>3①}\\{\frac{x+1}{2}<\frac{2-x}{3}+2②}\end{array}\right.$,
由①得:x>2,
由②得:x<$\frac{13}{5}$,
则不等式组的解集为2<x<$\frac{13}{5}$.
点评 此题考查了实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.-27的立方根为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 没有立方根 |
15.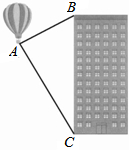 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )| A. | 80$\sqrt{3}$m | B. | 60$\sqrt{3}$m | C. | 40$\sqrt{3}$m | D. | 30$\sqrt{3}$m |
14.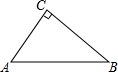 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
18.已知$\sqrt{12a}$是整数,则正整数a的最小值是( )
| A. | 2 | B. | 3 | C. | 6 | D. | 12 |
19.下列式子中,不属于二次根式的是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{{a}^{2}}$ | C. | $\sqrt{-7}$ | D. | $\sqrt{\frac{1}{2}}$ |